Yi (Joshua) Ren

🙏Many thanks to my supervisor @djsutherland.ml and the reviewers for their thoughtful suggestions and feedback.
📍Poster Hall 3+2B #376 on Fri, Apr 25 at 15:00
🎤Oral in Session 6A on Sat, Apr 26 at 16:30
📰https://arxiv.org/pdf/2407.10490
(12/12)

This wraps up the main story of our paper. 🎬
But there’s more coming—
🧠 Many RL + LLM methods (like GRPO) also involve negative gradients.
🎯 And a token-level AKG decomposition is even more suitable for real-world LLMs.
Please stay tuned. 🚀
(11/12)

With this setup, we can now explain some strange behaviors in DPO, like why the model's confidence on both the chosen and rejected answers drops after long training. 📉📉
Just apply force analysis and remember: the smaller p(y-), the stronger the squeezing effect.
(10/12)

Just like this!!!
(9/12)

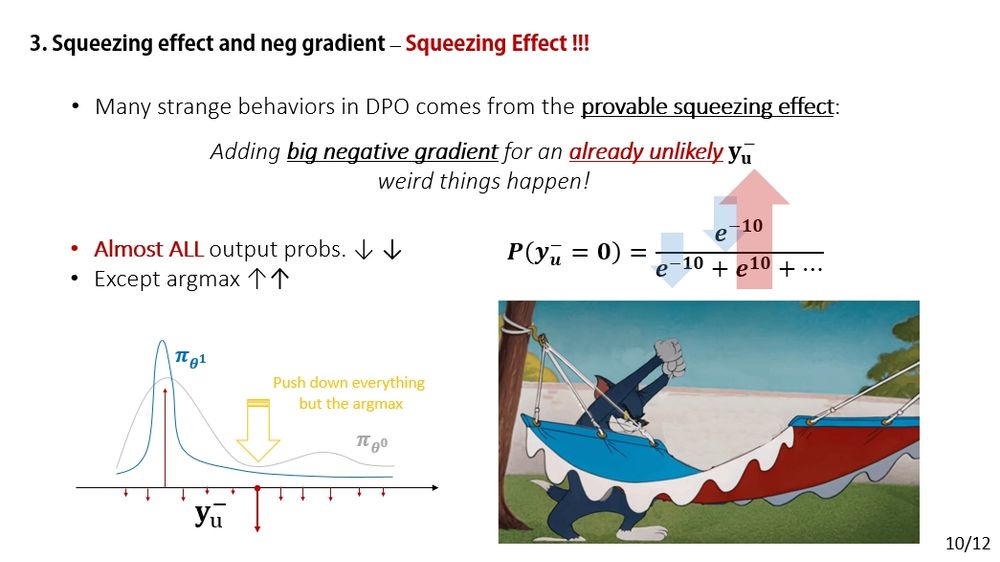
We formally show that, as long as you're using a softmax to produce probabilistic predictions, the squeezing effect is inevitable. And it gets stronger when p(y-) is smaller — the less likely an answer is (especially for off-policy), the harder all dimensions get squeezed.
(8/12)

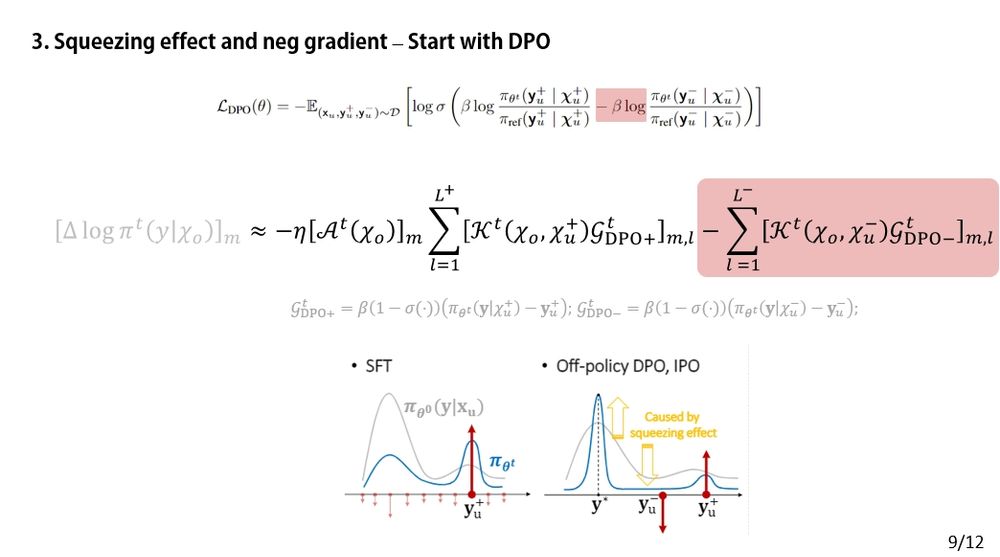
Now let’s switch gears to DPO — a more complex algorithm than SFT (as its AKG decomposition shows). But from a force analysis perspective, the story is surprisingly similar.
⚖️ The key difference? DPO introduces a negative gradient term — that’s where the twist comes in.
(7/12)

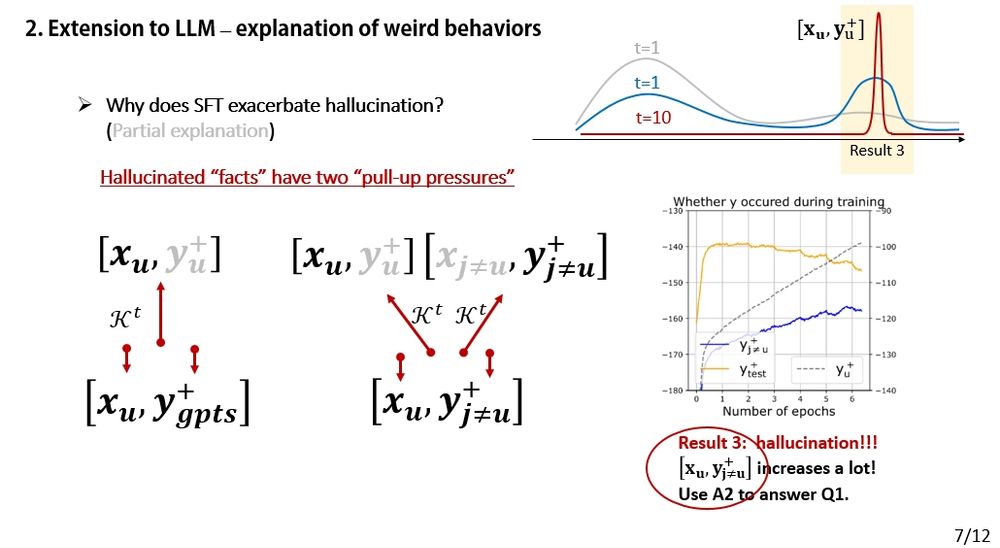
It also offers a possible explanation for a specific hallucination pattern in SFT:
🔍 The model uses facts or phrases from A2 when answering an unrelated Q1.
Why does this happen?
Just do a force analysis — the answer emerges naturally. 💡
(6/12)

Time to see how learning dynamics explains those weird behaviors. We observe a consistent trend: similar responses often rise in confidence, then fall.
📈📉 This aligns well with the force analysis perspective. (More supporting experiments in the paper).
(5/12)

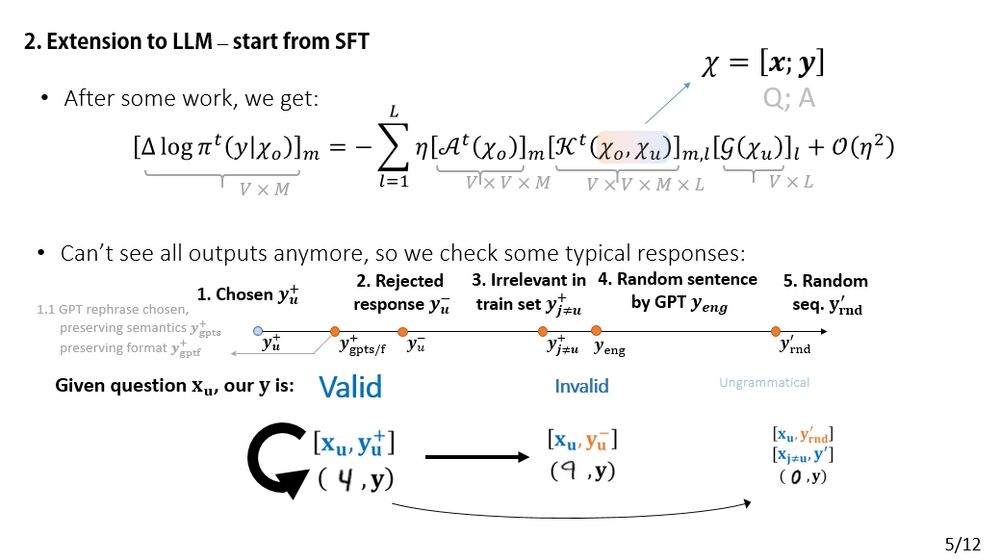
Now let’s analyze SFT!
The change in the model’s prediction can be decomposed (AKG-style). The input is a concatenation: [x; y]. This lets us ask questions like: “How does the model’s confidence in 'y-' change if we fine-tune on 'y+'?”
(4/12)

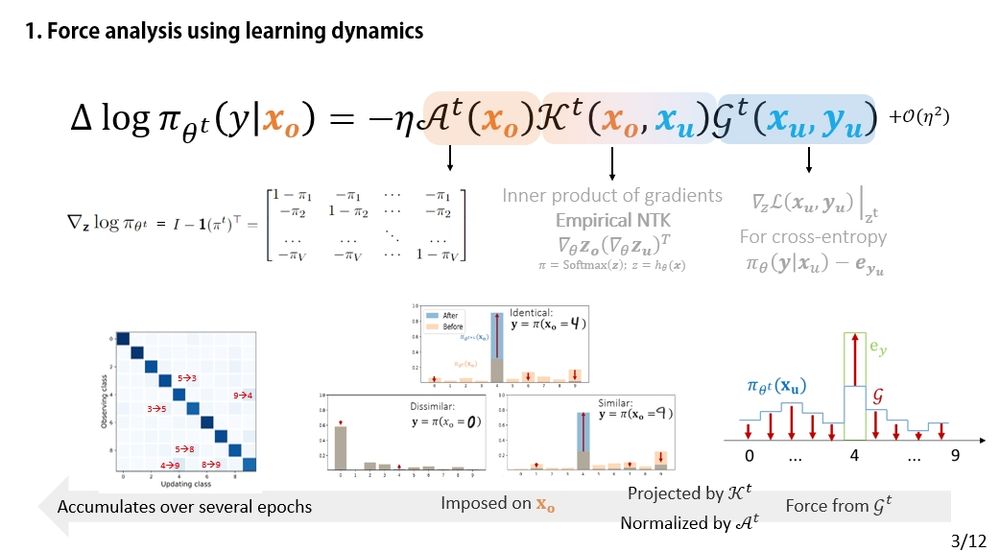
This toy example on MNIST helps you understand how it works: since 4 and 9 look similar from the model's perspective, learning 4 will make p(y=4 | 9) more likely. (More detailed discussions on simple classification tasks can be found here arxiv.org/pdf/2203.02485)
(3/12)

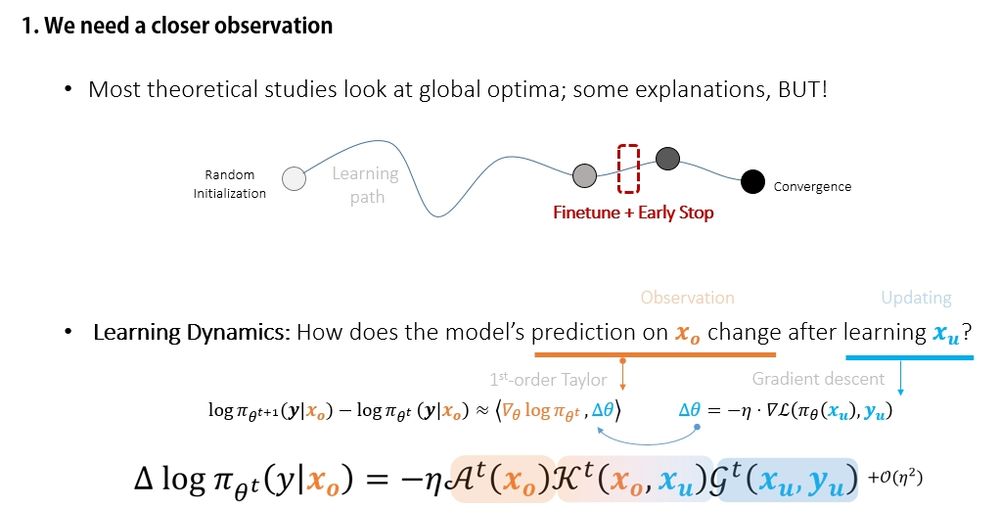
Instead of focusing on the global optimum, learning dynamics analyzes how the model behaves during training — one update at a time.
🧠 Think of the model's prediction as an object and each gradient update as a force acting on it.
(2/12)

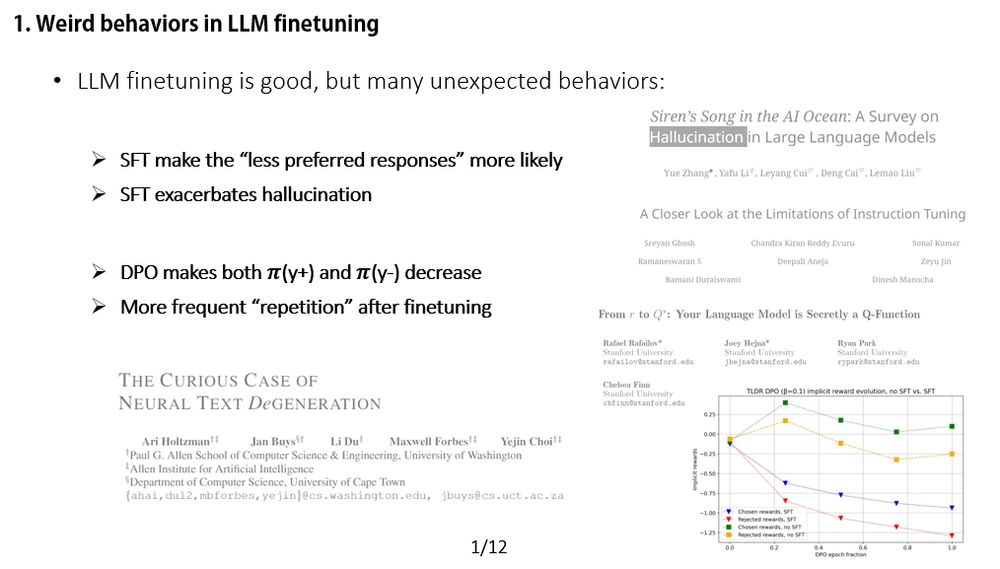
You might have seen some strange behaviors when fine-tuning LLMs.
🧩Prior work offers great insights, but we take a different angle: We dive into the dynamics behind these changes, step by step, like force analysis in physics. ⚙️
(1/12)

📢Curious why your LLM behaves strangely after long SFT or DPO?
We offer a fresh perspective—consider doing a "force analysis" on your model’s behavior.
Check out our #ICLR2025 Oral paper:

Learning Dynamics of LLM Finetuning!

(0/12)

We formally show that, as long as you're using a softmax to produce probabilistic predictions, the squeezing effect is inevitable. And it gets stronger when p(y-) is smaller — the less likely an answer is (especially for off-policy), the harder all dimensions get squeezed.
(8/12)

Now let’s switch gears to DPO — a more complex algorithm than SFT (as its AKG decomposition shows). But from a force analysis perspective, the story is surprisingly similar.
⚖️ The key difference? DPO introduces a negative gradient term — that’s where the twist comes in.
(7/12)

It also offers a possible explanation for a specific hallucination pattern in SFT:
🔍 The model uses facts or phrases from A2 when answering an unrelated Q1.
Why does this happen?
Just do a force analysis — the answer emerges naturally. 💡
(6/12)

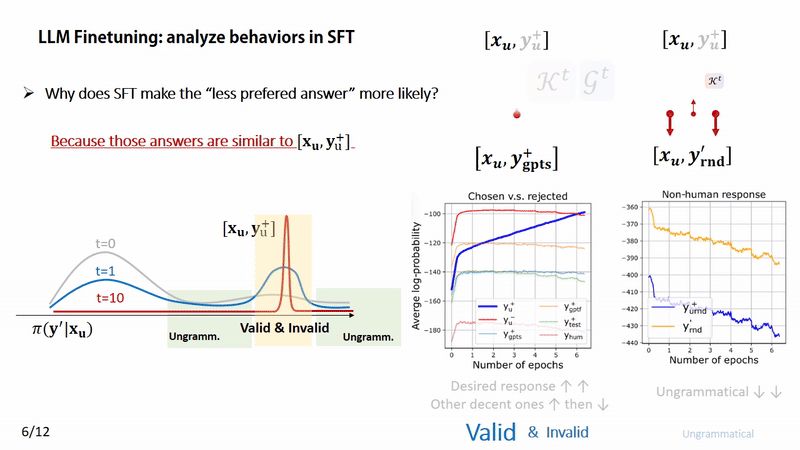
Time to see how learning dynamics explains those weird behaviors. We observe a consistent trend: similar responses often rise in confidence, then fall.
📈📉 This aligns well with the force analysis perspective. (More supporting experiments in the paper).
(5/12)

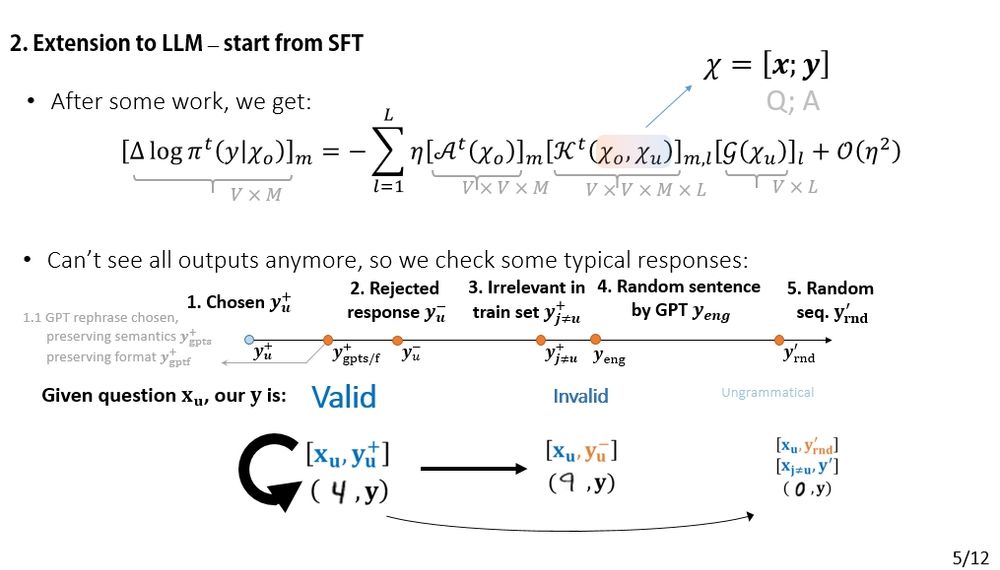
Now let’s analyze SFT!
The change in the model’s prediction can be decomposed (AKG-style). The input is a concatenation: [x; y]. This lets us ask questions like: “How does the model’s confidence in 'y-' change if we fine-tune on 'y+'?”
(4/12)

This toy example on MNIST helps you understand how it works: since 4 and 9 look similar from the model's perspective, learning 4 will make p(y=4 | 9) more likely. (More detailed discussions on simple classification tasks can be found here arxiv.org/pdf/2203.02485)
(3/12)

Instead of focusing on the global optimum, learning dynamics analyzes how the model behaves during training — one update at a time.
🧠 Think of the model's prediction as an object and each gradient update as a force acting on it.
(2/12)

You might have seen some strange behaviors when fine-tuning LLMs.
🧩Prior work offers great insights, but we take a different angle: We dive into the dynamics behind these changes, step by step, like force analysis in physics. ⚙️
(1/12)