Tamás Görbe

“springs, strings, airplane wings

steel beams, light beams, and water streams

building sways, ocean waves, and sound waves...”

— Peter Lax (1926-2025)

Planets ~ Springs | The Newton-Hooke Duality and Beyond Everything’s a spring!? When I’m in a cheeky mood, I like to tease first-year physics students by telling them that for physicists everything is a spring1 or a (potentially infinite) co…

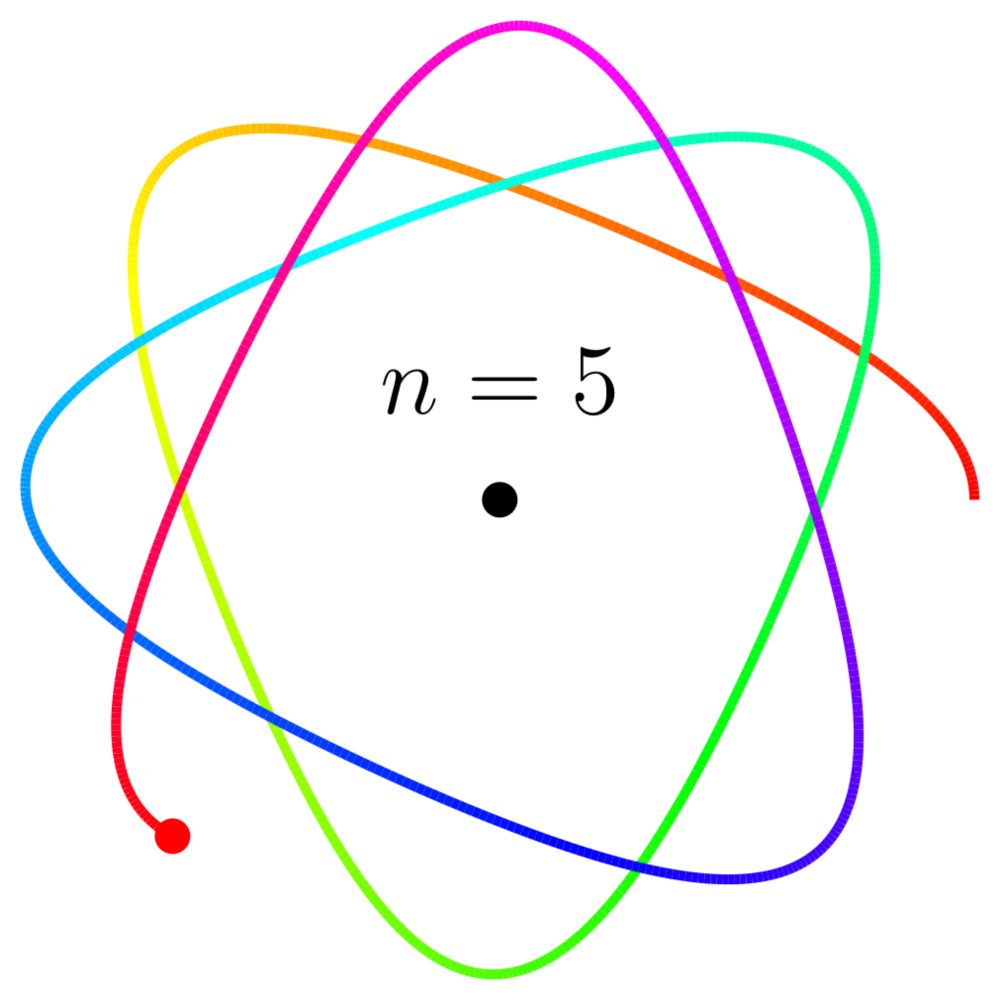
Planets ~ Springs | The Newton-Hooke Duality and Beyond tamasgorbe.wordpress.com/2025/05/09/p...

Me (15 years ago):
Definitions < Theorems

Me (now):
Definitions > Theorems

YouTube video by Tamás Görbe Measuring π using a Planimeter #PiDay 2025

Happy Pi Day everyone!

I measured π using a planimeter to celebrate #PiDay

youtu.be/1M0d2Hw9r10

Science is prose, Mathematics is poetry.

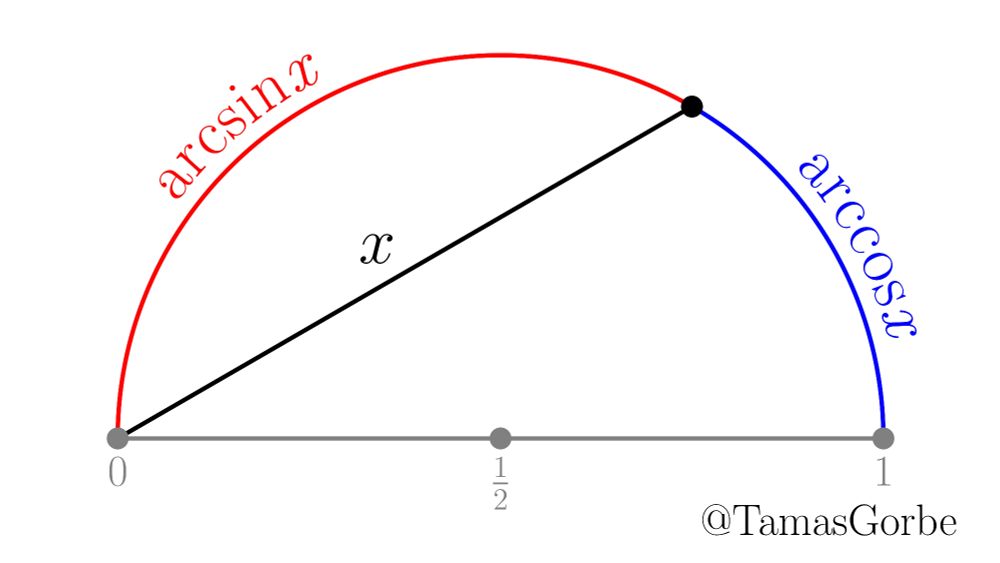
The inverse trig functions arcsin and arccos as actual arc lengths

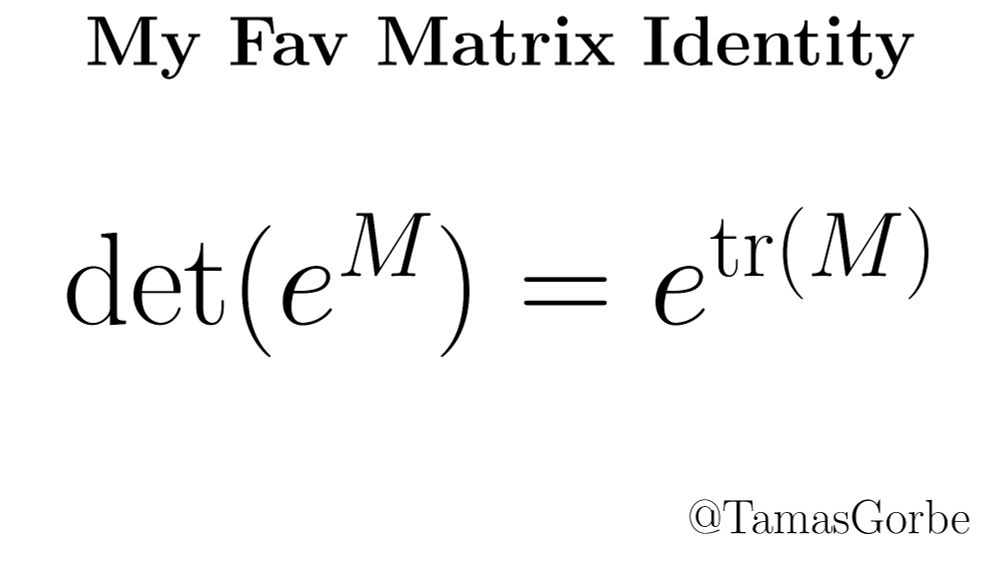
My favourite matrix identity

the determinant of the exponential equals the exponential of the trace

Fibonacci Numbers via Matrix Multiplication

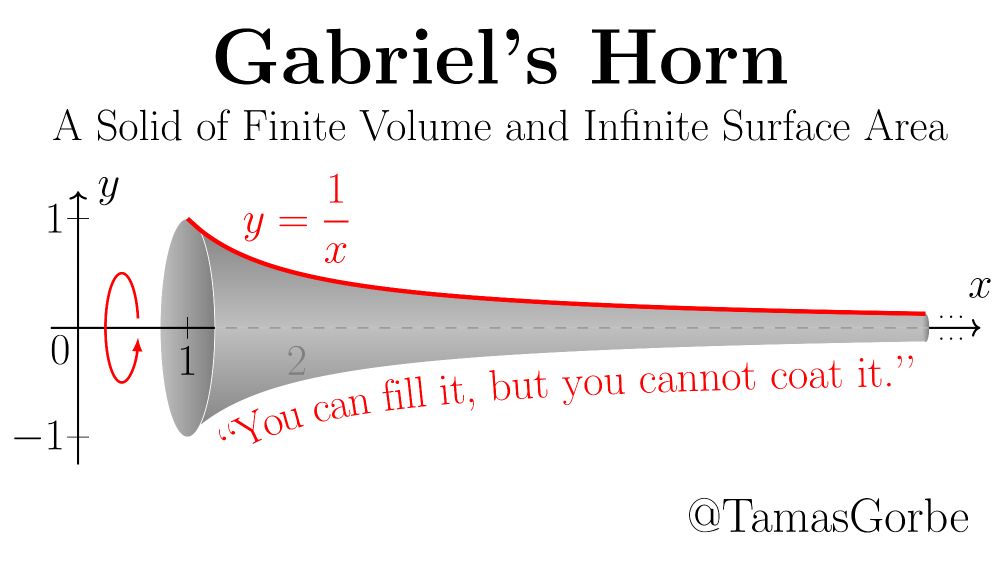
Gabriel's Horn is a solid you get by rotating the hyperbola y=1/x (with x>1) about the x-axis.

Having finite volume (π) and infinite(!) surface area, it leads to the apparent paradox:

"You can fill it with paint, but you cannot coat it."

Pascal's Determinant

Any square matrix cut from the top corner of Pascal's Triangle has determinant 1.

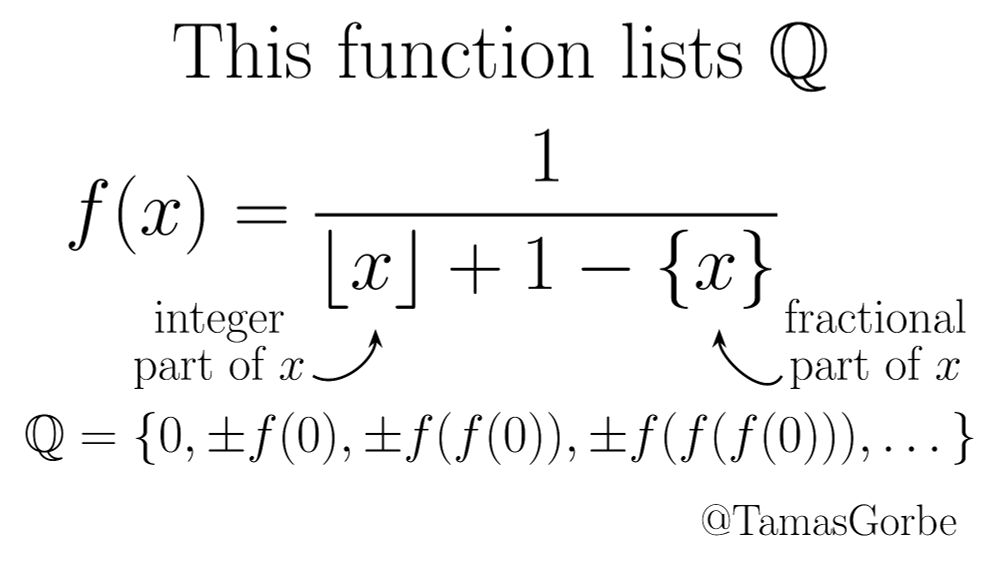
Consider the function

f(x) = 1 / ( ⌊x⌋ + 1 − {x} )

and the sequence of numbers

0, f(0), −f(0), f(f(0)), −f(f(0)), f(f(f(0))), −f(f(f(0))), ...

Congratulations, you've just listed every rational number exactly once!

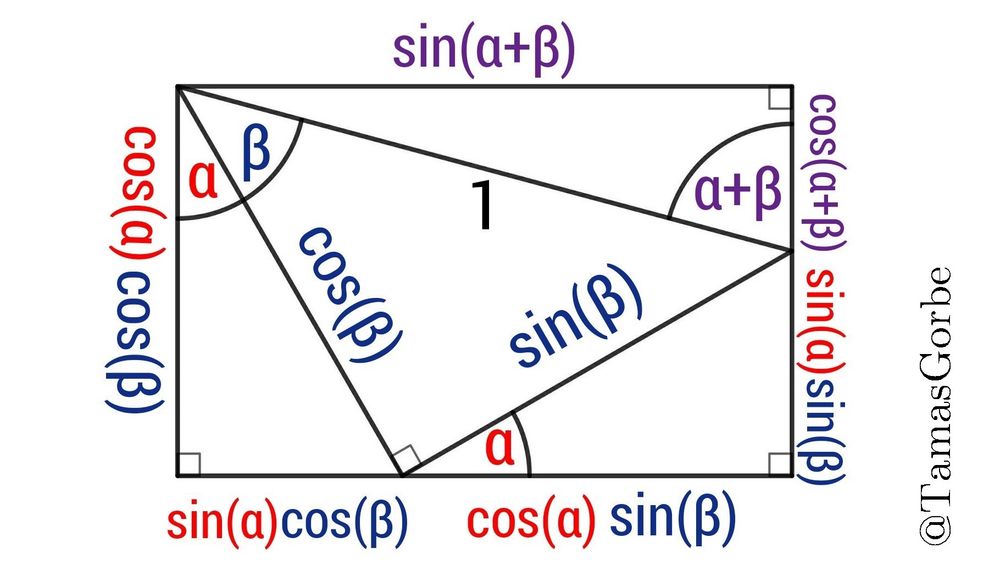
Trigonometric Addition Formulas
− a visual proof −

sin(α+β) = sin(α)cos(β) + cos(α)sin(β)

cos(α+β) = cos(α)cos(β) – sin(α)sin(β)

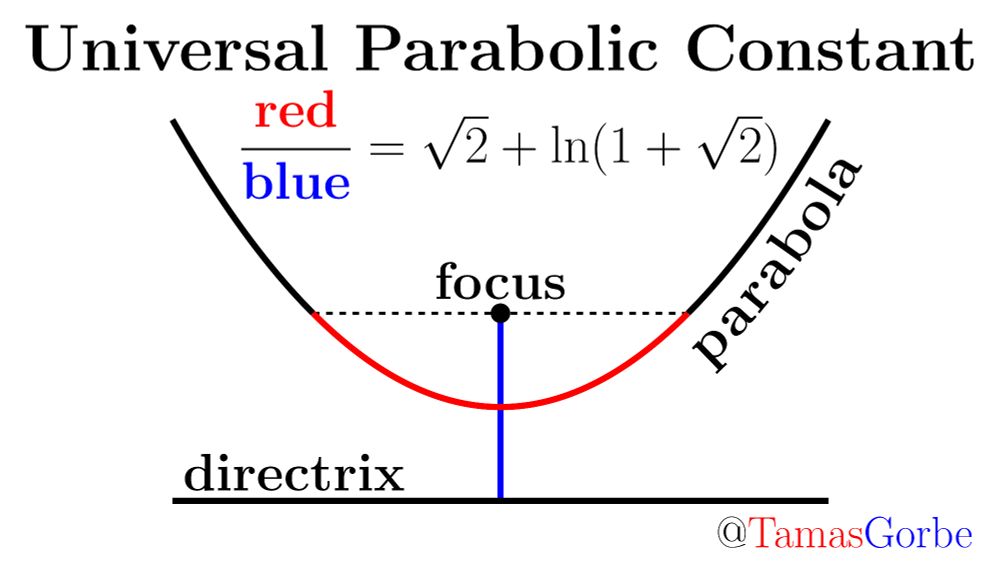
Everyone knows that all circles are similar. But did you know that all parabolas are similar?

The ratio of the red arc and the blue focal segment is
√2 + ln(1+√2) = 2.29558...
for every parabola.

This is the universal parabolic constant, the “π of parabolas”.