laura cui

La brea tar pits

Oil is the most Lovecraftian thing that actually exists.

You're telling me that there's a black ichor under the earth made from the ancient dead, whose burning can realize all the dreams of man, but only at the price of slowly returning the earth to its primordial state?

happy to share some examples privately if that'd be helpful!

that's fair! it's possible I've just been lucky to have people (friends, mentors, parents) close to me go through this successfully

interesting, maybe I have a lower bar but I wouldn't say it's particularly uncommon or frowned upon in my circles

is it not?

People take for granted the fact that mangos are so delicious, but most don’t know that every logical mango is made out of many physical mangos.

Are you a computer scientist and don't know what an OTOC is, but want to understand the problem solved in the recent Nature paper by Google Quantum AI? We wrote a 2-page note that explains the motivation and presents a simplified version of the problem for any input size.
scirate.com/arxiv/2510.1...

MIT rejects Trump administration deal for priority federal funding MIT is one of the nine schools that were asked to agree to adopt conservative priorities and policies in exchange for funding perks.

This is what courage in the face of authoritarianism looks like. No university should take Trump's bribe & surrender their integrity — bending the knee to a bully only feeds the beast & puts ALL our rights at risk.

Others should follows MIT’s example ASAP.

+ in the non-adaptive setting, there exist ensembles w/ natural spectral distributions whose dynamics look random in O(1) time ⌛

These results complement each other & highlight subtleties in formulating random models which capture the properties of physical dynamics 🔎 ✨

8/8

However, when this constraint is relaxed, we show it is possible to construct ensembles of quasi-local time-independent Hamiltonians which generate pseudorandom dynamics!

These ensembles can also be efficiently simulated assuming the existence of quantum-secure OWFs 💻

7/8

On the other hand, in [2] we consider time evolution dynamics when factoring in uncertainty in H 🤔

When the connectivity of the system is known, we show that the dynamics of any ensemble of local Hamiltonians, at any time scale, can be distinguished from a random unitary.

6/8

To prove this, we construct Hamiltonians which embed arbitrary Turing machines.

Under standard cryptographic assumptions, there exist Hamiltonians whose long-time dynamics perform computations that are out of reach for (& can be distinguished from) any efficient circuit 🤖

5/8

While some models admit energy-conserving PRUs, we show that in general no efficient construction exists even for local 1D spin chains ⛓️

Not only that, determining if there exist energy-conserving PRUs for a given family of local 1D Hamiltonians is in general undecidable!

4/8

This leads us to define energy-conserving ensembles [1] which are maximally random w/ the constraint [U, H] = 0. In general, this is the same as averaging over all times.

We then ask, when can we efficiently construct energy-conserving pseudorandom unitaries (PRUs)? 🔋

3/8

We first observe that for any time-independent Hamiltonian H, the dynamics are diagonal in the energy eigenbasis.

If H is local, we can also efficiently distinguish it from random unitary dynamics by preparing states with non-zero energy and checking if H is conserved ⚡

2/8

When can we use random unitaries to (efficiently) model physical dynamics? 💻 ⚛️

Excited to share a couple of works with Liang Mao, Fernando Brandão, Robert Huang, Thomas Schuster in which we explore this question!

[1] arxiv.org/abs/2510.08448

[2] arxiv.org/abs/2510.08434

1/8

some of us are also too young to understand the myspace vs facebook analogy...

I've complained a couple times about the lack of physics community here but not done much about it! New commitment: I'll post one interesting arXiv paper a day until things are better.

(To the folks who follow me for non-physics science policy, don't worry; plenty more of that reporting to come.)

The Ginsburg Center for Quantum Precision Measurement @caltech.edu now stands 4 stories high. Opens summer 2026.

I don't have anything against it in principle! but you could argue that working with instead of against community norms is better for visibility & communication of your results

counterpoint: it's fun when academics refuse to write a paper so you see everyone cite a blog post or youtube video instead

How fast can (pseudo)random unitaries be implemented on a quantum computer? O(1) time suffices (provided you can do things like intermediate measurements)! This -and more- is thanks to a superfun collaboration with Ben Foxman, @nat-parham.bsky.social, and @franvasco.bsky.social (all PhD students!).

Nicole’s guide to writing research statements Sunflowers are blooming, stores are trumpeting back-to-school sales, and professors are scrambling to chart out the courses they planned to develop in July. If you’re applying for an academic job t…

Useful advice from @nicoleyh11.bsky.social.

quantumfrontiers.com/2025/08/10/n...

Random Unitaries in Constant (Quantum) Time Random unitaries are a central object of study in quantum information, with applications to quantum computation, quantum many-body physics, and quantum cryptography. Recent work has constructed unitar...

In exciting new work with Ben Foxman, @nat-parham.bsky.social , and @henryyuen.bsky.social we show that t-designs and pseudorandom unitaries are implementable in constant (quantum) time!

arxiv.org/abs/2508.11487

according to other sources commercial panels were only at around 15% a decade ago (when I was learning about energy science in high school the quoted number was around 10%)

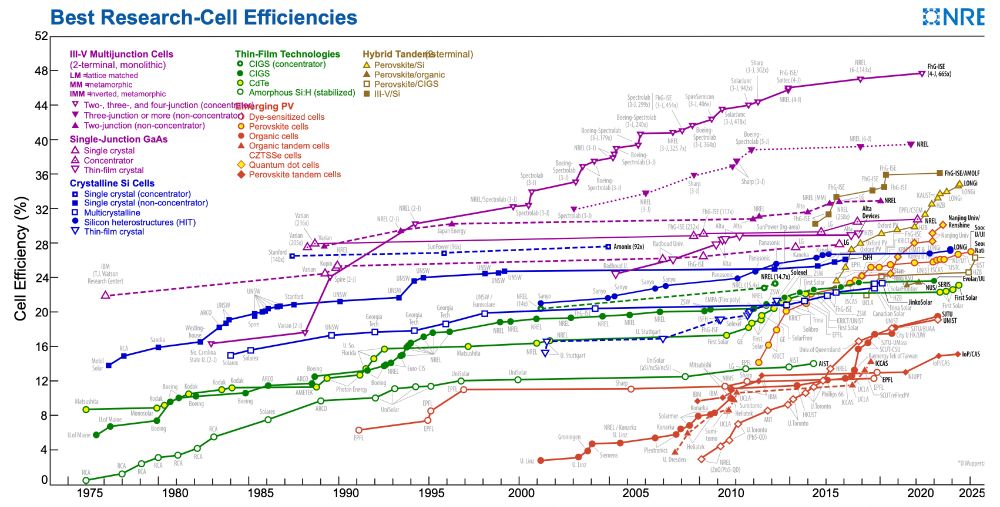
also according to wikipedia the record for solar cell efficiency performance in r&d testing is close to 48% which is crazy when you compare to photosynthesis (~5%) and ecological trophic levels (~10%)

video & comments make some very sharp points ("quantum computers are to classical computers what planes are to cars" @ f5673-t1h)

... but I'm actually more amazed by what she said about modern solar panels 🤯 25% efficiency for commercially available panels in 2025 is crazy

One more day, one more chance to pretend that I understand the word "topological"

Adding one more note which I missed from the magic-augmented Cliffords paper

tough crowd