Thibaut Boissin

So in short:

AOL preconditioning (fused + re-tuned) -> 1 iter saved

Better convergence, singular values closer to 1

Kernel tweak removes extra memory load

This gives ~1.6x speedup, ~3x vs plain torch. 🚀

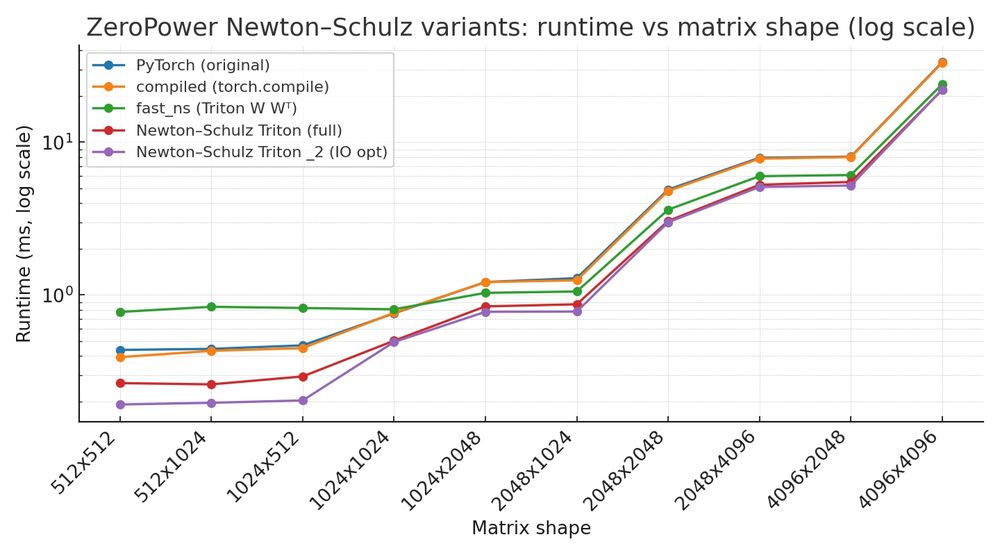
Bonus: I spotted redundant memory loads in the 3rd NS line.
Wrote a small kernel to optimize bandwidth ->more free speed.

Problem 1: AOL adds extra cost.
Fix: fuse AOL's operation with an existing NS step -> essentially free.

Problem 2: NS isn’t tuned for "almost orthogonal" inputs.
Fix: re-tune parameters with a genetic algorithm that is aware of the preconditioning.

The inspiration comes from
Bernd Prach's Almost Orthogonal Layer (AOL).
It gives a cheap way to make a matrix "almost orthogonal."

Not great for full orthogonalization, but much better than rescaling -> perfect as a preconditioner for NS.

The key idea: reduce the number of NS iterations.
How? By pre-conditioning the input matrix.

This makes the algorithm converge faster without losing precision.

GitHub - thib-s/flash-newton-schulz: My attempt to improve the speed of the newton schulz algorithm, starting from the dion implementation. My attempt to improve the speed of the newton schulz algorithm, starting from the dion implementation. - thib-s/flash-newton-schulz

here’s the code: github.com/thib-s/flash... (I'll do a PR soon in Dion/Muon)

And here’s how I squeezed out the extra gain

I used a mathematical trick to pre-condition the matrix, allowing to shave one iteration of the algorithm. This is not only faster, but also unlocks better convergence, with singular values closer to 1.

Good news: I managed to get an extra 1.6x speedup of the Newton Schulz algorithm (which is at the core of Dion/Muon). It reaches nearly a 3x speedup over the plain torch implementation !

What is the S_n^++ ?

It's crazy to think that I spent years using bjork&Bowie algorithm with 25 iters, and within a year, we got NS alg, an optimized set of parameters to run it in 5 iter, and triton kernels.

Large matrices are already compute bounded so the gain is small for those, so I will work to add fp8 support (once current code is consolidated).
I'll do a PR into the Dion repo when ready !

Sharing my journey to learn triton: still wip but io optimization yields some decent runtime improvement (around 25% on 512x512) on Newton Schulz (as used in Dion/Muon).

A meme showing on the first line "how it started" with a screen capture showing a nice triton's tutorial, followed by "how it's going" with complex code about fp4 quantization for microscaling in some linear algebra algorithm.

My journey with Triton

Open Question: Does FP4 make fine-tuning easier or harder? On one side, fp4 weight might demand high precision gradients, on the other, it might be super compliant with QLoRA, what do you think ?

Robustness Check: Training in FP4 stress-tests hyperparameters and initialization quality.
If your model converges, you have robust, well-conditioned weights and gradients.
The model will likely be more resistant to input noise.

Not "Pure" FP4: FP4 rarely stands alone. It's usually accompanied by per-row or per-column scaling factors (FP8/FP16). Gradients are often accumulated at higher precision (FP16/FP32), making ultra-low precision practical.

Efficiency Boost: Halving precision (FP8 → FP4) allows doubling parameters with roughly similar FLOPs. But benefits can be even bigger because:
- Larger vector sizes enhance activations utilization.
- Lower precision floating-point math itself adds beneficial non-linearities.

It's likely better to have a larger model in FP4 than a smaller one in FP8 (if you can train it):
- Improved non-linearity utilization with larger feature vects
- Enhanced hardware utilization on blackwell archs.
- Stress-test your training, yields models robust to input noise

more below

Pay attention to your loss: understanding misconceptions about 1-Lipschitz neural networks Lipschitz constrained networks have gathered considerable attention in the deep learning community, with usages ranging from Wasserstein distance estimation to the training of certifiably robust class...

Funny enough, this is the content of Appendix N (page 34) of arxiv.org/abs/2104.05097 😂

This makes me wonder what happens in standard training: when your training loss increases, does it mean that optimization failed? Or that, thanks to weight decay, the network’s (unknown) Lipschitz constant got lower and the network is just getting more robust? 🤷

This has deeper implications: two networks with different initialization, batch order, or data augmentation end up learning the same function (same answers, same errors, both in train and val), even though the weights are completely different!

The change in the Lipschitz constant makes the network more accurate (when increased) or more robust (when decreased). Unlike traditional classification, robust classification with a Lipschitz net has a unique minimizer once the Lipschitz constant is set.

The Lipschitz constant of a network impacts its robustness, but what happens when you change it during training? Here, we train 16 networks with a fixed Lipschitz constant at first, then increase or decrease it by a factor of two mid-training.

Beyond robustness: Lipschitz networks = stability.
Different inits, different seeds, different weights—same function.
A thread 🧵

Some bad, but creative, training losses 👌