Michael Birch

If Friday the 13th is bad luck then is Friday the 31st good luck?

A hand of 7 basic Plains.

I guess this hand would be spookier if it was all Swamps, but 7 lands is still pretty scary! Happy Halloween!

mtg-lib/duskmourns-claim at main · birchmd/mtg-lib Contribute to birchmd/mtg-lib development by creating an account on GitHub.

The full code for the simulation is available on GitHub if anyone is curious.

github.com/birchmd/mtg-...

I don't think any of this data is useful in practice; this deck is clearly not competitive in standard (where aggro decks can regularly win on turn 4 or 5 and control decks will have ample answers for the namesake card). But I had fun putting all this together regardless!

Other mulligan heuristics will have to be a topic for future research.

The deck can also lose by decking before killing the opponent. This happens around 0.1% of the time. Losing to a goldfish is kind of funny, but again the simulation doesn't ever attack, which obviously makes a difference.

Since this is a combo deck, I tried adding mulligan heuristics to try to have Claim in the opening hand. But this also made things worse, increasing the average to 11.57. I am not sure why this makes things worse and I think it should be true that a mulligan heuristic exists to improve performance.

The average is winning on turn 11.38 (+/- 0.01). The scry/surveil logic used when playing lands is important. If I disable this in the simulation (always top) then the average increases by almost half a turn to 11.86. I think this means including those lands in the mana base is good deck building!

About 61% of the time, the deck wins between turns 7 and 10 (inclusive). It wins on turn four 0.03% of the time. The turn 4 win happens by playing Claim on turn 3, hitting a big spell on end step then playing a second copy on turn 4 with both copies hitting big spells (7 x 3 = 21 damage).

Histogram showing the frequency that the Duskmourn's Claim deck wins at different turn numbers. It has a bell-like shape, but with a longer tail at higher values (not symmetric around the mean). The bulk of the distribution exists between turns 7 and 12 (inclusive).

That said, I think this simulation should still give a bit of a sense of how quickly the deck deals damage on average and how important certain decisions are. The main result is the plot showing the distribution of turn number on which the deck wins (deals lethal damage with Claim).

First, some caveats. The simulation is vastly simplified relative to the actual complexity of playing magic. Notably, there is no combat because the main goal of this deck is to drain the opponent out with Duskmourn's Claim. Also the decision making follows simple (not optimal) heuristics.

I thought it would be fun to try to simulate playing this deck against a goldfish opponent. I'll share my results in a thread.

I also had fun playing the deck myself of Arena.

Thanks for sharing it @mtgcreativecombos.bsky.social !

MTG Arena stats during Edge of Eternities. My favourite format was draft, I was in the 80th percentile of games played, 95th percentile of quests gold, and 90th percentile daily wins gold. I reached diamond 4 rank in constructed and gold 3 in limited.

#MTGArenaStats during Edge of Eternities

The Magic: the Gathering Arena Achievements page on the Color Masteries tab showing 9/10 completed in all five colors.

I have managed to become a jack of all colors, master of none on #MTGArena
This feels like an achievement in its own right.

The Pi Day in March is far inferior to the one today. Not only is M.DD (3.14 in the case of Pi Day) a terrible date format, but 22/7 is a better approximation!

So happy Pi Day to all who celebrate!

That said, I can't complain about having two excuses to talk about math :)

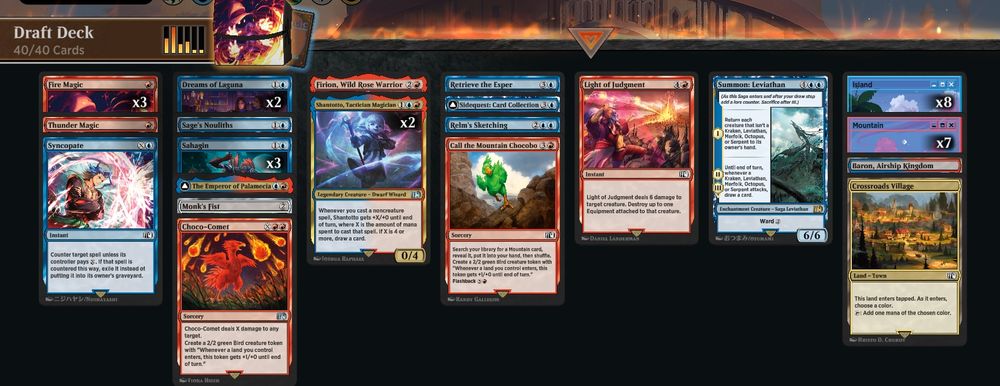
Deck 3 Fire Magic (FIN) 136 1 The Emperor of Palamecia (FIN) 219 1 Firion, Wild Rose Warrior (FIN) 137 2 Dreams of Laguna (FIN) 50 1 Sage's Nouliths (FIN) 70 1 Retrieve the Esper (FIN) 68 1 Summon: Leviathan (FIN) 77 1 Monk's Fist (FIN) 265 1 Thunder Magic (FIN) 165 1 Call the Mountain Chocobo (FIN) 131 1 Crossroads Village (FIN) 276 1 Light of Judgment (FIN) 144 1 Choco-Comet (FIN) 132 2 Shantotto, Tactician Magician (FIN) 241 1 Relm's Sketching (FIN) 67 3 Sahagin (FIN) 71 1 Sidequest: Card Collection (FIN) 73 1 Syncopate (FIN) 80 1 Baron, Airship Kingdom (FIN) 273 8 Island (SLD) 1469 7 Mountain (SLD) 1471 Sideboard 1 Coral Sword (FIN) 134 1 Sleep Magic (FIN) 74 1 Minwu, White Mage (FIN) 26 1 Aerith Rescue Mission (FIN) 5 1 Snow Villiers (FIN) 33 1 Adventurer's Inn (FIN) 271 1 Sidequest: Play Blitzball (FIN) 158 1 Sabotender (FIN) 153 1 Haste Magic (FIN) 140 1 Laughing Mad (FIN) 143 1 Opera Love Song (FIN) 147 1 Dovin's Veto (FCA) 51 1 Vincent's Limit Break (FIN) 126 1 Item Shopkeep (FIN) 142 1 Rook Turret (FIN) 69 1 Quina, Qu Gourmet (FIN) 194 1 Sharlayan, Nation of Scholars (FIN) 288

A record of 7-2 in Premier Draft Final Fantasy on Magic: the Gathering Arena.

It's no secret now that blue-red spells is a good deck in #MTGxFINALFANTASY draft. But it's still satisfying when a good version comes together and you get 7 wins on #MTGArena !

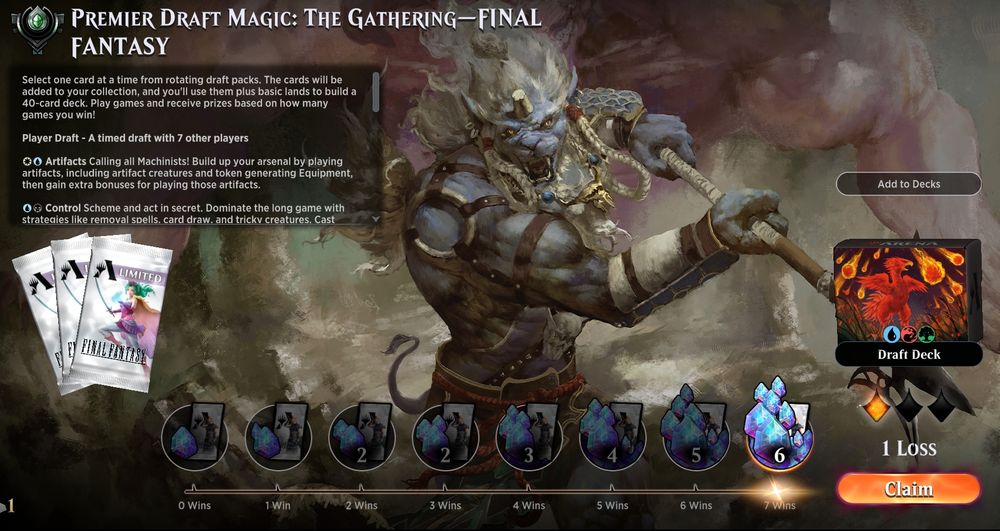
7-1 record in Premier Draft on Magic: The Gathering Arena.

Deck 1 Choco-Comet (FIN) 132 1 Quina, Qu Gourmet (FIN) 194 4 Gysahl Greens (FIN) 190 1 Airship Crash (FIN) 171 1 Blitzball Shot (FIN) 176 1 Tellah, Great Sage (FIN) 244 1 Lightning Bolt (FCA) 40 1 Bartz and Boko (FIN) 175 1 Queen Brahne (FIN) 149 1 Gongaga, Reactor Town (FIN) 280 1 Call the Mountain Chocobo (FIN) 131 1 Warrior's Sword (FIN) 169 1 Ride the Shoopuf (FIN) 197 1 Light of Judgment (FIN) 144 1 The Regalia (FIN) 267 1 Summon: Esper Ramuh (FIN) 161 1 Torgal, A Fine Hound (FIN) 208 1 Summon: G.F. Ifrit (FIN) 163 1 Summon: Fenrir (FIN) 203 1 Summon: Titan (FIN) 204 1 Guadosalam, Farplane Gateway (FIN) 281 1 Summon: Fat Chocobo (FIN) 202 1 Island (SLD) 1469 7 Mountain (SLD) 1471 7 Forest (UST) 216 Sideboard 1 Thief's Knife (FIN) 81 1 Absolute Virtue (FIN) 212 1 The Emperor of Palamecia (FIN) 219 1 Battle Menu (FIN) 9 1 Giott, King of the Dwarves (FIN) 223 1 Rydia's Return (FIN) 198 1 Blitzball Shot (FIN) 176 1 Cloudbound Moogle (FIN) 11 1 Vincent's Limit Break (FIN) 126 1 Monk's Fist (FIN) 265 1 Town Greeter (FIN) 209 1 Rabanastre, Royal City (FIN) 287 2 Gigantoad (FIN) 187 2 Commune with Beavers (FIN) 182 1 Snow Villiers (FIN) 33

Ah Chocobo Spells, a classic archetype of #MTGxFINALFANTASY draft. Still good enough for 7 wins on #MTGArena

All joking aside, this deck was super fun to draft and play. And FF is a fun draft format because it has synergies allowing you build decks outside the seeded archetypes.

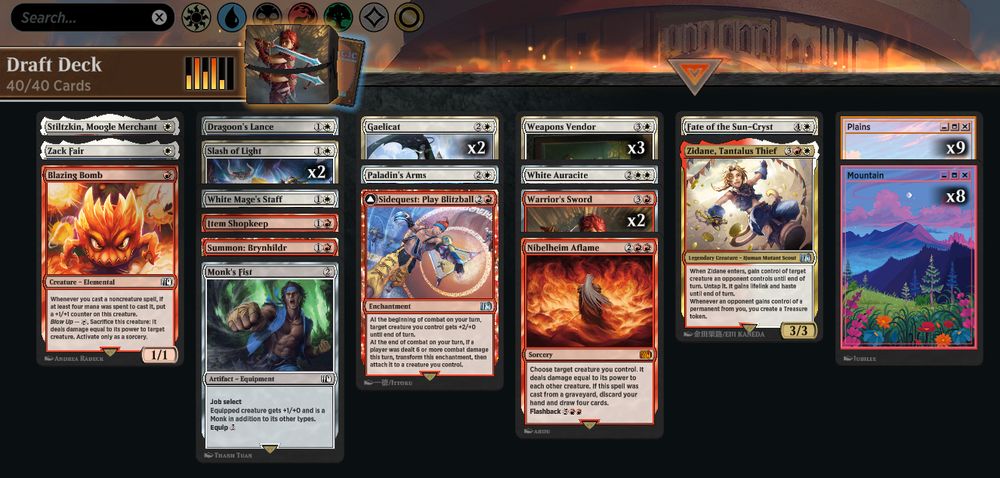
Deck 1 Stiltzkin, Moogle Merchant (FIN) 34 9 Plains (SLD) 1468 1 Zack Fair (FIN) 45 1 Blazing Bomb (FIN) 130 8 Mountain (SLD) 1471 1 Dragoon's Lance (FIN) 17 2 Slash of Light (FIN) 32 1 White Mage's Staff (FIN) 42 1 Item Shopkeep (FIN) 142 1 Summon: Brynhildr (FIN) 160 1 Monk's Fist (FIN) 265 2 Gaelicat (FIN) 22 1 Paladin's Arms (FIN) 28 1 Sidequest: Play Blitzball (FIN) 158 3 Weapons Vendor (FIN) 40 1 White Auracite (FIN) 41 1 Fate of the Sun-Cryst (FIN) 19 1 Zidane, Tantalus Thief (FIN) 251 1 Nibelheim Aflame (FIN) 146 2 Warrior's Sword (FIN) 169

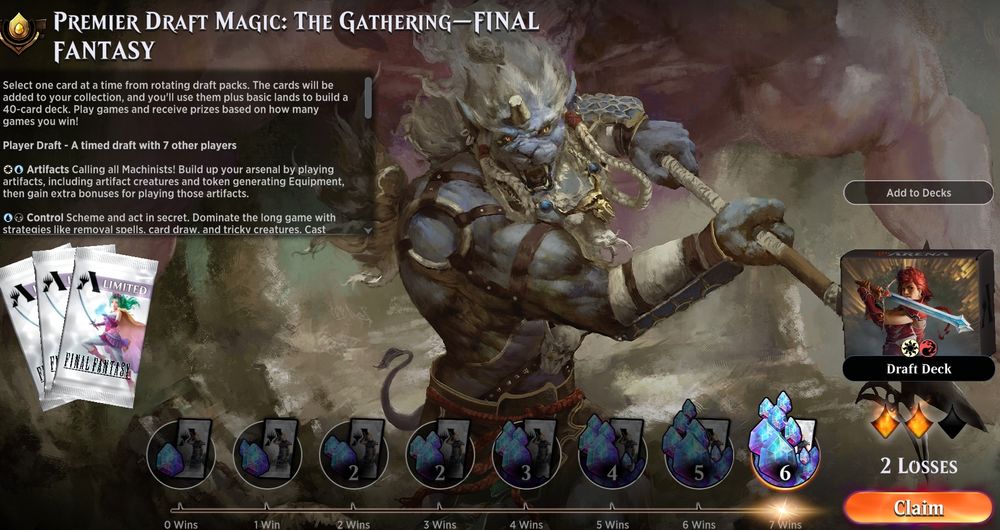
7-2 record in Premier Draft Magic: The Gathering Final Fantasy

My first 7 wins in #MTGxFINALFANTASY draft on #MTGArena !

If you're wondering where these came from, the real ones are titles presented at ETAPS 2025, which I had the pleasure of attending this year. I didn't present anything myself, but I enjoyed the presentations I saw and I'm looking forward to digging more into formal verification!

Disclaimer: this is just a bit of fun! I am not disparaging any of the real talk titles. They are clear and technically accurate, which is exactly what you want from an academic talk title.

C. Two-sorted algebraic decompositions of Brookes's shared-state denotational semantics

D. Reachability for Nonsmooth Systems with Lexicographic Jacobians

Poll: Which one of the following four talk titles is fake?

A. First-Person Choreographic Programming with Continuation-Passing Communications

B. Verification of Hybrid Hierarchical Systems via Approximate Abstraction Refining

(continued in 🧵)

So I suspect, though haven't looked at the numerical data to double check, that away from (0.5,0.5) a+b is positive so that the equilibria are unstable and thus allows the state to move towards the stable equilibrium in the center. And this is what the numerical trajectories showed as well.

I realized one more thing about the linearization and stability analysis. There is a whole line of equilibria y=x and the linearization applies to all of them. Since -1 is always an eigenvalue, the line is stable along one direction. The other eigenvalue is a+b, which changes along the line.

So if your deck is a little better than your opponent (p>0.5) then on average you add cards to your deck, making it worse until they're evenly matched. This is reversed if you're a little behind your opponent. And so the game continues until a large enough variation randomly pushes someone to win.

I went into a lot of mathematical details above, but I didn't give any intuitive explanation. The idea is adding cards to your deck is bad (lower chance of finding high value cards). That negative is worse than the positive of adding a slightly above average card to move up the average of your deck.

This figure shows the result of simulating 20 million games of War. To describe what is being plotted we first need to know the mathematical model I used for the analysis. Let's assign each card in the deck a value 2 through 14. Then the outcome of a round of the game is determined solely by comparing these values. And we can measure how well a player is doing by considering the total value of cards in their deck. A value of 416 means that player has all the cards. We also track the the number of cards each player has. A player with all the cards as 52. Without loss of generality, we can focus on player 1 since if player 1 has a deck value V containing N cards then player 2 has a deck value of 416 - V and 52 - N cards, so dynamics of player 2 are easily deduced from the dynamics of player 1. To make our lives easier, we rescale the variables: x = V/416 and y = N/52. Note x and y are both in the range [0, 1]. We'll derive equations for how x and y change in the next figure, but for now we have enough context to say what is plotted in this figure. It is the (x, y) state space for the games. Each colored line is the average over many games with the same (V, N) initial conditions. All lines start at y=0.5 since each player begins with half the deck. They can start at different points in the x direction because the cards are randomly assigned to the players (so player 1 may get more or less high-value cards). All the trajectories move diagonally until they approach the line y = x, then they all follow this line to the center point (0.5,0.5). Thus we see the games evolving to this steady state where they will stay forever, as described in the main post. Now let's see if we can explain this numerical result with our mathematical model.

To explain this plot we develop our mathematical model further. Recall from the previous figure we have the state variables V and N, and their rescaled versions x and y. Suppose player 1 has a probability p of winning the next round of the game. Clearly p depends on V and N, we'll come back to that later (that's what this plot is about). For now we have the following equation for how V changes: dV = p (416 - V)/(52 - N) - (1 - p) V/N i.e. if player 1 wins the round then they add value to their deck equal to the average value of their opponent's deck, and if they lose then they lose value from their deck equal to their average value. Similarly, the equation for how N changes is: dN = p - (1 - p) = 2p - 1 i.e. N goes up by 1 with probability p and down by 1 with probability 1-p. The equations are cleaner in terms of our rescaled variables: 52dx = p[(1-x)/(1-y) + x/y] - x/y 52dy = 2p - 1. First we can notice that there is an equilibrium (dx=dy=0) when p=x=y=1/2. I.e. both players have half the deck. And this is exactly what we observed in the numerical simulation. The differential equations are non-linear, but we can check if this equilibrium is stable by linearizing the equations. A little calculus reveals: 26dx = (a - 1)(x - 0.5) + (b + 1)(y - 0.5) 26dy = a(x - 0.5) + b(y - 0.5) where a = dp/dx and b = dp/dy, both evaluated at x=1/2,y=1/2. The eigenvalues of the matrix for this linear system are -1 and a+b, so to make progress we need to know the value of these derivatives. Maybe there is a way to get them analytically, but we can get them numerically from the same data that gave the first figure. For each (V,N) state we count how often player 1 won the round to estimate the probability p. Plotted in this figure is p as a function of x for different (fixed) values of y. Lines for values of y lower than 0.5 are redder and those higher are greener. There are multiple nearly parallel diagonal lines with positive slope.

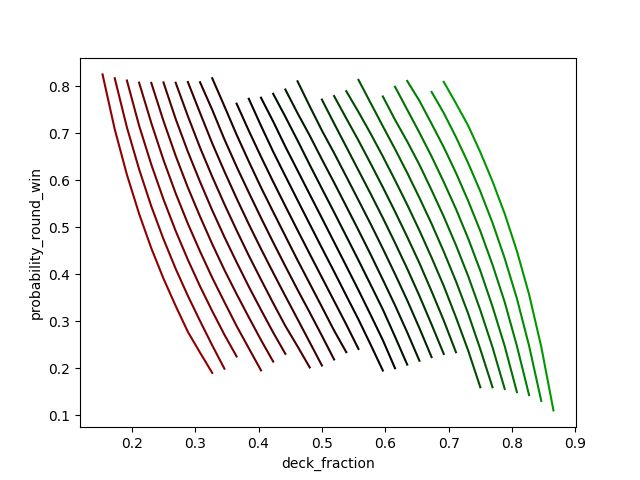
Continuing our analysis from where we left off with the previous figure, this plot shows p as a function y for different (fixed) values of x. Once again lines corresponding to values of x less than 0.5 are redder while those that are greater are greener. There are multiple nearly parallel diagonal lines with negative slope. The further the lines get from 0.5 the more curved they become. The previous plot can be used to get the value of a = dp/dx at x=y=0.5, and this plot gives the value of b = dp/dy at x=y=0.5. The results are a = 2.6 b = -2.7. So the sum is a+b=-0.1 and thus both eigenvalues of our linearized set of differential equations are negative. Therefore we have shown the equilibrium is stable! This agrees with the results of the simulation where all the state-space trajectories converged on the equilibrium. Notice that the differential equations in our model did not account for wars (the mechanic which gives the game its title). They only include deck changes in the case one player wins the round immediately. I think the reason this does not impact our results is because wars are very infrequent events and therefore do not have a qualitative impact on the mean field theory.

The results are shown in the figures below. The alt text of the images discusses the methodology in greater detail.

(the game will end with probability 1; as long as you shuffle the cards sometimes). But this analysis shows it happens only because of random fluctuations. That's why it can take a while! And also why it's good for distracting children.

With a combination of numerical simulation and analysis of differential equations, I conclude that the mean field theory for this game says the game will go on forever with both players having about half the deck. Of course a real game will eventually end

The main question we want to answer is about the dynamics of how the cards flow back and forth between the players. To avoid the details of actual cards we employ mean field theory (useful in epidemiology for example).

War (card game) - Wikipedia

Let's do some mathematical modelling for fun! 🧵

War is a simple card "game" sometimes played by children. It's really more of an activity actually because there are no decisions for the players to make, but this makes it easier to model.

en.wikipedia.org/wiki/War_(ca...