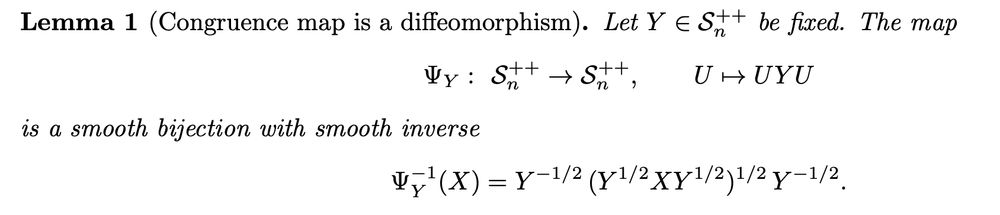Gabriel Peyré

Yes I agree. In 1D the global convergence result is known bc the energy is displacement convex, but not in higher dimension. So it could be the case that there exists adversarial targets.

Also, the curves were wrong, they did not start from the first set of points ... As a side comment, it is quite amazing that they are almost not stuck in local minima and almost all end up at the target points.

I have updated my "Optimal Transport for Machine Learners" repository with a Pytorch illustration of Wasserstein gradient flows on pairwise interaction functionals (MMD distances) github.com/gpeyre/ot4ml

It is true! Means that can be approximated by first taking harmonic and then arithmetic means are exactly the scalar Kubo-Ando means. A homogeneous mean m is of this type iff r \mapsto m(1,r)/r is operator monotone on. For m(x,y)=((x^p+y^p)/2)^{1/p}, this holds precisely when -1 \le p \le 1.

It is in the closure for p in {-1,0,1} so it must be true for all p in [-1,1]... or maybe not...

What is the set of "means" one can approximate using only arithmetic and harmonic means ? For instance the geometric mean belongs to this closure, but can one approximate any mean sandwitched between the two?

KL to a Gaussian target, (entropic) Wasserstein distance to a Gaussian. This invariance makes Gaussians an exceptionally handy test case.

Thought of the day: It is somewhat mysterious why Gaussians remain stable under the particle-minimizing flow (i.e. the Wasserstein gradient flow) for so many widely used energies: entropy, Fisher information, quadratic interaction potentials, functionals depending only on mean and covariance,

#Communiqué 🗞️ La médaille d'or 2025 du CNRS est décernée à Stéphane Mallat, mondialement reconnu pour ses travaux autour des mathématiques appliquées au traitement du signal et à l’intelligence artificielle. 👏

👉 cnrs.fr/fr/presse/en...

#TalentsCNRS 🏅

Symmetric and positive (invertible) matrices.

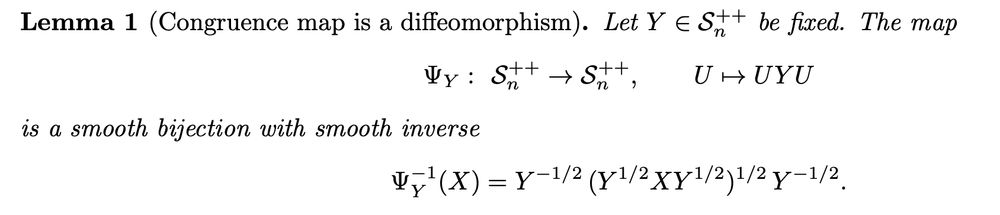
To meditate while resting on the beach...

Fun (...) fact: the only linear operators on matrices that preserves the rank are X->AXB, where A and B are invertible (with X->X^T in the square case). This was apparently first proved (?) in 1959 by Marcus and Moyls.

scPRINT | v1.0 | Virtual Cells Platform scPRINT is a cell foundation model, also called a Large Cell Model (LCM), trained on single-cell RNA sequence (scRNAseq) data from more than 50M human and mouse cells available through CZ CELLxGENE. Based on the transformer architecture, the model is fully open source and reproducible, with multiple checkpoint sizes available from 2M to 100M parameters. scPRINT demonstrated high performance for genome-wide cell-specific gene network inference when benchmarked against state-of-the-art models (e.g., scGPT, Geneformer v2, GENIE3). In addition, scPRINT has various zero-shot capabilities, including cell embedding, cell label prediction (e.g., cell type, sex, disease), and gene expression imputation, highlighting its potential as a versatile tool for single-cell analysis.

scPRINT is now finally on the Chan Zuckerberg Institute's Model Hub! 🎉 🧬 🌈 It is one more way you can use this cell foundation model to embed, denoise, predict cell type, get gene networks from your data from scratch, or fine-tune it on your own application / usecase: virtualcellmodels.cz...

Oui je pense

Le prochain Data Science Colloquium à l'ENS, jeudi 12 juin, sera donné par David Louapre d'Ubisoft, "What modern AI and neuroscience can bring to non-playing characters in video games". David c'est bien sûr également le vulgarisateur scientifique de www.youtube.com/scienceetonn...

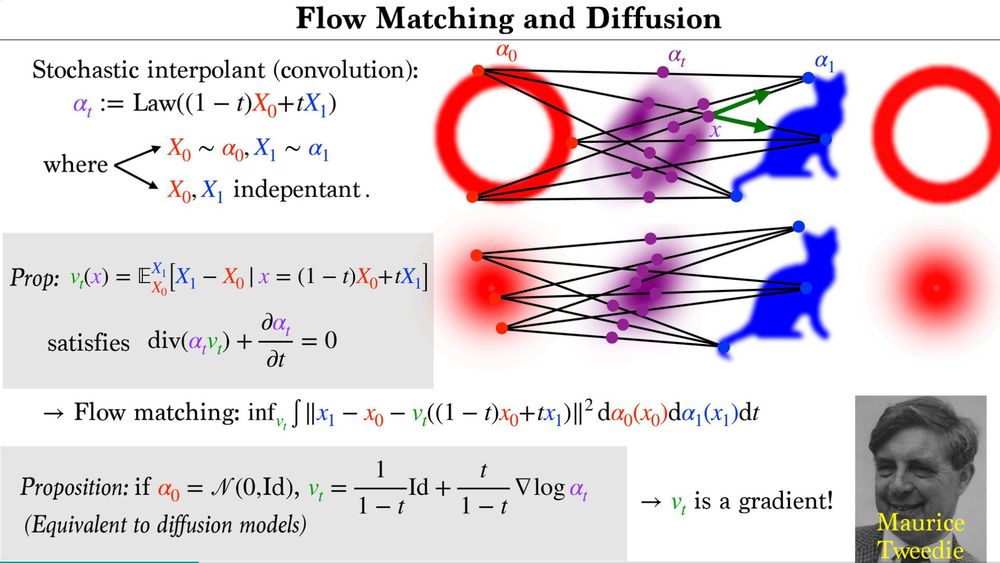
If one of the two distributions is an isotropic Gaussian, then flow matching is equivalent to a diffusion model. This is known as Tweedie's formula. In particular, the vector field is a gradient vector, as in optimal transport. speakerdeck.com/gpeyre/compu...

Cyril Letrouit | Collège de France

The course is currently running on Wednesdays, you should go if you are in Paris and interested in OT! www.college-de-france.fr/fr/personne/...

Lectures note for the course of Cyril Letrouit at Collège de France on the quantitative stability of optimal transport.
www.imo.universite-paris-saclay.fr/~cyril.letro...

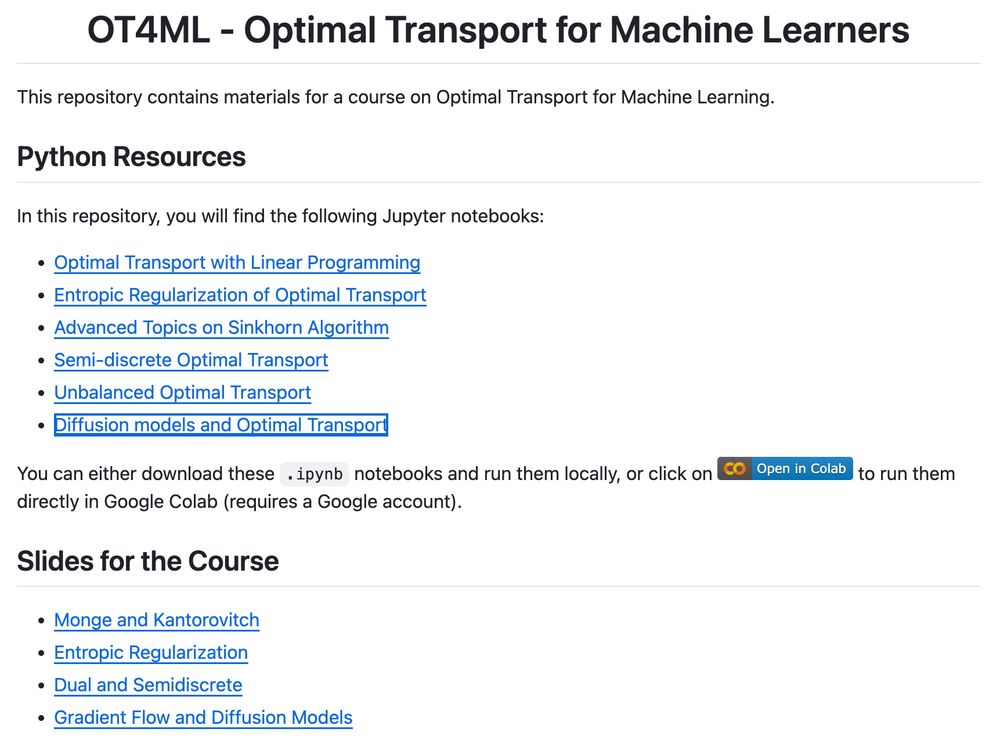
I have cleaned up the notebooks for my course on Optimal Transport for Machine Learners and added links to the slides and lecture notes. github.com/gpeyre/ot4ml

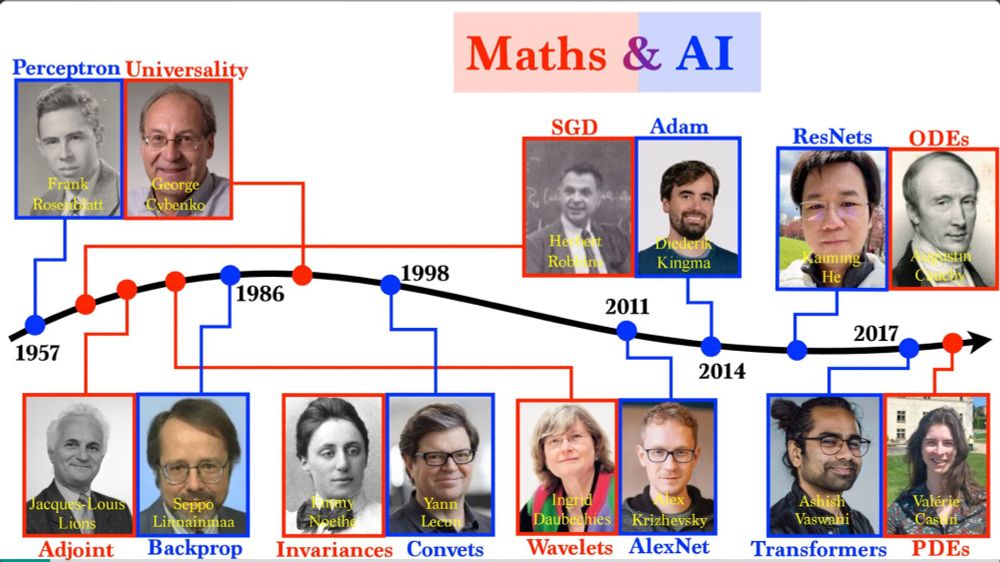
I have updated my slides on the maths of AI by an optimal pairing between AI and maths researchers ... speakerdeck.com/gpeyre/the-m...

Mon article sur les maths de l’IA est paru dans la gazette de la smf smf.emath.fr/publications...
La version en anglais est sur arxiv
arxiv.org/abs/2501.10465

Optimal Transport for Machine Learners Optimal Transport is a foundational mathematical theory that connects optimization, partial differential equations, and probability. It offers a powerful framework for comparing probability distributi...

I have cleaned a bit my lecture notes on Optimal Transport for Machine Learners arxiv.org/abs/2505.06589

Announcing : The 2nd International Summer School on Mathematical Aspects of Data Science
mathsdata2025.github.io
EPFL, Sept 1–5, 2025

Speakers:
Bach @bachfrancis.bsky.social
Bandeira
Mallat
Montanari
Peyré @gabrielpeyre.bsky.social

For PhD students & early-career researchers
Apply before May 15!

Applications are 📣OPEN📣 for #PAISS2025 THE AI summer school in #Grenoble 1-5 Sept! Speakers so far @yann-lecun.bsky.social @dimadamen.bsky.social @arthurgretton.bsky.social @gabrielpeyre.bsky.social @science4all.org A. Cristia J. Revaud M. Caron J. Carpentier M. Vladimirova ➡️ paiss.inria.fr

The AI for Science summer school, coorganized by CNRS and U of Chicago will be in Paris, June 30th to july 4th, register asap if you want attend!
datascience.uchicago.edu/events/ai-sc...

Futur best seller!

Characterizing finely the decay of eigenvalues of kernel matrices: many people need it, but explicit references are hard to find. This blog post reviews amazing asymptotic results from Harold Widom (1963!) and proposes new non-asymptotic bounds.
francisbach.com/spectrum-ker...

I am biased toward the SURE, I won’t take the risk to estimate without Stein.

⚡️Check out our workshop tomorrow at @lpiparis.bsky.social, great speakers (@gabrielpeyre.bsky.social, @sdascoli.bsky.social, @samillingworth.com & many more) will cover Theory and Applications of Generative AI + Connexions with neuroscience 🧠
And there's food 🍰
➡️ genai-conference-website.vercel.app

YouTube video by Mathématiques et informatique - Collège de France Génération de données en IA par transport et débruitage (5) - Stéphane Mallat (2024-2025)

Video de l’exposé niveau collège (en français...) youtu.be/F-MRgm6OE54