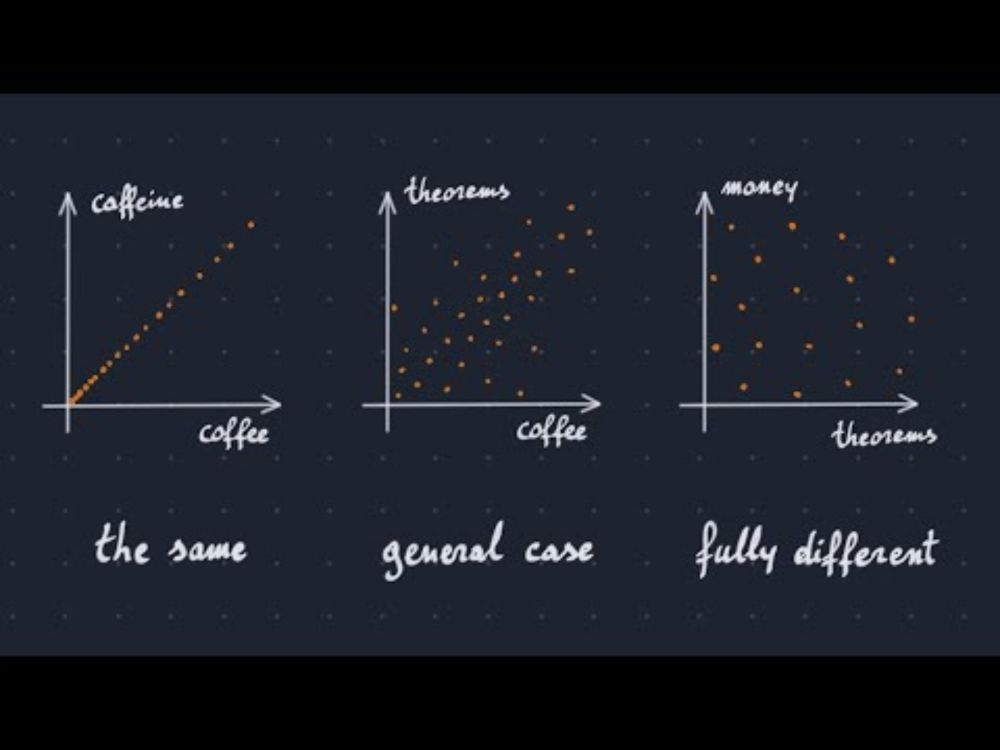
A categorical definition of independence!
Here is a recording of the talk I gave at CT 2025, for anyone who might have missed it.
youtu.be/ls6zOX8L1eI
@paolopmath.bsky.social
Mathematician & Math Teacher

A categorical definition of independence!
Here is a recording of the talk I gave at CT 2025, for anyone who might have missed it.
youtu.be/ls6zOX8L1eI

New paper out!
arxiv.org/abs/2508.01146
The document that started categorical probability, part of secret work from 1962, has reappeared, together with new commentaries of its author, Bill Lawvere.
lawverearchives.com/wp-content/u...
Thanks to Tobias Fritz and to the Lawvere Archives for the work.
It seems that it's the year of double categories.
21.07.2025 15:00 — 👍 0 🔁 0 💬 0 📌 0I'm excited to be in Bologna for the week!
(If anyone is here and wants to meet, write me an email.)

Me, every time the EU "wants to attract researchers":
05.05.2025 18:56 — 👍 2 🔁 0 💬 0 📌 0
We start in 10 minutes!
02.05.2025 08:50 — 👍 0 🔁 0 💬 0 📌 0
What are point-free measurable spaces, and what is their quantum equivalent?
Great work by Tobias Fritz and Antonio Lorenzin.
arxiv.org/abs/2504.13708

We finally have the strong law of large numbers in Markov categories.
arxiv.org/abs/2503.21576

To all my UK-based mutual are into 'cybernetics', I very strongly recommend this exhibition in London.
www.tate.org.uk/whats-on/tat...

New great work by Dario Stein.
arxiv.org/abs/2503.02477

What do Beck-Chevalley monads have to do with conditional probability?
arxiv.org/abs/2502.14941
Wait, espresso doesn't make you think about math?
30.01.2025 09:56 — 👍 1 🔁 0 💬 1 📌 0If there was anybody competent in charge in Europe we would be passing emergency legislation this week so that starting next week we poach every scientist from the US who was previously funded by NSF, NIH etc. Oh well, we can dream.
28.01.2025 12:20 — 👍 5 🔁 4 💬 1 📌 0
Never forget that you do can do natural gradient descent in Haskell!
github.com/alex404/goal
Using "many" for something that's counted by a natural number and "much" for something that's counted by a real number (and a unit, usually) is actually a good approximation.
14.01.2025 07:58 — 👍 4 🔁 0 💬 0 📌 0Excited to be in Seattle for the JMM!
Besides ACT today and categorical probability on Saturday, which sessions are my fellow category theorists attending?
(Reposting)
One thing that we don't stress enough is that the correspondence morphisms-programs is true also *outside* the cartesian closed (=functional) case.
Morphisms are programs, regardless of whether they form their own object/type or not.
I don't know if this models all the examples you have in mind, but in every monoidal category, the monoidal unit is canonically a monoid.
22.12.2024 13:18 — 👍 1 🔁 0 💬 1 📌 0Lyckönskningar!
20.12.2024 23:39 — 👍 1 🔁 0 💬 0 📌 0Yes. (Or at least a decategorification thereof.)
16.12.2024 12:53 — 👍 2 🔁 0 💬 1 📌 0I need the 2-version of that. Something like "We give coherent bijections between the following structures..."
05.12.2024 10:46 — 👍 2 🔁 0 💬 0 📌 0
Here's a lecture at MIT on Markov categories, symmetries, and generative AI by Rob Cornish and myself.
youtu.be/ozN4zLEUCgs?...
#touchdesigner #streamdiffusion #bananas

New paper on Markov categories, proving Aldous-Hoover categorically, by Leihao Chen, Tobias Fritz, Tomáš Gonda, Andreas Klingler, Antonio Lorenzin.
arxiv.org/abs/2411.12840
The smartest thing the EU can do now is release a ton of funding for scientists, and relative visas. And I mean immediately.
12.11.2024 13:47 — 👍 1 🔁 0 💬 0 📌 0
My book is out!
www.worldscientific.com/worldscibook...