@robinhouston got some interesting responses and I think I see the situation a little more clearly now, though I'd still like to know what exactly "breaks" if one restricts to the "natural" subcategory of tree morphisms in [ω^op,Δ₊]. I'd be happy if anyone here knows the answer to that.
30.07.2025 15:13 — 👍 0 🔁 0 💬 0 📌 0
Original post on social.sciences.re
Every logician knows about Peirce’s law, this curious tautology equivalent to the law of excluded middle that uses only the implication connective. Less known is that around 1896, Peirce invented the first diagrammatic proof system in history, predating string diagrams in category theory and […]
29.07.2025 09:40 — 👍 1 🔁 2 💬 0 📌 0

After a year I left Chicago to go to Göttingen where I hoped that the environment of Hilbert would give more encouragement to my study of logic and rigor. By then I must have vaguely begun to see that a good proof consisted of more than just rigorous detail, because there was also an important element of plan for the proof -- the crucial ideas, which, over and above the careful detail, really make the proof function and get to the desired end. I clearly recall sitting in a vast lecture room listening to Edmund Landau lecture on Dirichlet series. As always, Landau's proofs were simply careful lists of one detail after another, but he gave this detail with such exemplary care that I could both copy down in my notebook all the needed detail and enter in the margin some overarching description of the plan of his proof (a plan which he never directly revealed).
Then I came gradually to the insight that proofs in mathematics combined rigorous detail and overall plan -- and that overweening attention to the precision of detail could, as in the case of \emph{Principia}, wholly hide the plan. There arose with me the notion that the necessary rigor could be codified and simplified, so as to be made almost automatic. If only the automatic could be properly described and organized, then the essential ideas of the proof would come through. This idea of organizing the \emph{plan} of a proof in a formal way was evidently the germ of my thesis.

I explained it to them in Vienna, where I thought that Rudolph Carnap would be more sympathetic. Instead, I thought very hard in spurts about a thesis. A decisive spurt came on April 18--22, when I finally worked out a plan of the final thesis. In an exuberant letter of April 26th to my mother I wrote:
\begin{quote}
``Perhaps I have time to tell you a bit about my new discovery. It's a new symbolic logic for \emph{mathematical proofs.} It applies, as far as I can see now, to all proofs in all branches of mathematics (a rather big order!). It makes it possible to write down the proof of a theorem in a very much shorter space than by the usual methods, and at the same time it makes the proof very much clearer. In essence, it eliminates practically \emph{all} the long mechanical manipulations necessary to prove a theorem. It is only necessary to give \emph{leading ideas} of the \emph{proof.} In fact, once these leading ideas are given -- together with a few directions -- then it becomes possible to compute \emph{from} the leading ideas just what the \emph{proof} of the theorem will be. In other words, once these leading ideas are given, all the rest is a purely mechanical sort of job. It is possible to define once and for all how the job is to be carried out (the general definition depends essentially upon the abstract methods I have been developing for the past year).''
\end{quote}

On this basis, I described exactly a number of the routine steps in a proof, giving each a label, as for example:
\begin{quote}
\emph{Inf schrumpf}: To prove a theorem $L \supset P$, search for a prior theorem of the form $M\supset N$, where $L$ is a ``special case'' of $M$ and $P$ the corresponding special case of $M$.
\emph{Sub inf schrumpf}: Given a prior theorem $M\supset N$, one can conclude that $L\supset L'$, where $L'$ is obtained from $L$ by replacing every ``positive'' component of the form $M$ by a new component $N$.
\emph{Sub Def}: Substitute the definitions.
\emph{Identität}: Use one of the standard identities of algebra (or of the propositional calculus).
\emph{Sub Theorem \#20.43}: Use the cited theorem, in the (only) possible way.
\emph{$x = C$ fixieren}: Given a premise $(\exists x)L(x)$, assert $L(C)$ for some suitable ``constant'' $C$.
\emph{Halbnorm}: Move a quantifier $\exists x$ or $\forall x$ to the front of an expression.
\end{quote}
All told the thesis gives twenty or twenty-five of such rules (listed at the start of Chapter VII), and then observes that many proofs can be ``abbreviated'' by listing in order the rules to be applied. In this sense, the thesis gives a formal definition of a routine proof.
A lesser known fact about Saunders Mac Lane is that he wrote a thesis in logic, completed in 1933 at Göttingen under the direction of Bernays and Weyl. I'm at the library and pulled out a copy of "Saunders Mac Lane : Selected Papers", which in addition to […]
[Original post on mathstodon.xyz]
25.07.2025 12:10 — 👍 1 🔁 1 💬 1 📌 0
Original post on mathstodon.xyz
In my whole career as a university educator, there have been two major disrupting events: Covid and generative AI.
None of them made the students any favour.
Or the educators.
But for the educators these are only headaches (big headaches, granted).
For the students it is much worse.
When […]
09.07.2025 18:42 — 👍 1 🔁 4 💬 0 📌 0
Original post on mathstodon.xyz
I've mentioned this paper by @pamellies and myself before, and the main contents are by now 1.5-3 years old, but I'm happy to report that the final version of the paper has at last been published by LMCS:
* The categorical contours of the Chomsky-Schützenberger representation theorem […]
19.05.2025 12:56 — 👍 0 🔁 1 💬 0 📌 0
![[dubious text from "Celebrity Birthdays" site.]
Donald Knuth is one of the most popular and richest Mathematician who was born on January 10, 1938 in Wisconsin, Wisconsin, United States. Mathematician and engineer who was arguably most recognized as the Professor Emeritus at Stanford in Palo Alto, California.
Henry Suzzallo once studied at Stanford University, where he served as the Professor Emeritus.](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:t7ajsa37yphkf2vp6ydd3mvk/bafkreig4r4kvrmmnnyb5cxnwgbu3hfszwnqf5m2olopjp4w5vryxhhixem@jpeg)
[dubious text from "Celebrity Birthdays" site.]
Donald Knuth is one of the most popular and richest Mathematician who was born on January 10, 1938 in Wisconsin, Wisconsin, United States. Mathematician and engineer who was arguably most recognized as the Professor Emeritus at Stanford in Palo Alto, California.
Henry Suzzallo once studied at Stanford University, where he served as the Professor Emeritus.
![[dubious text from "Celebrity Birthdays" site.]
Donald Knuth Net Worth
Net Worth $5 Million
Source Of Income Mathematician
House Living in own house.
Donald Knuth is one of the richest Mathematician from United States. According to our analysis, Wikipedia, Forbes & Business Insider, Donald Knuth 's net worth $5 Million. (Last Update: December 11, 2023)](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:t7ajsa37yphkf2vp6ydd3mvk/bafkreih37wldurjtgripjrreb7gfzy7hbde7xme6cegdeiwtov3wdoiz34@jpeg)
[dubious text from "Celebrity Birthdays" site.]
Donald Knuth Net Worth
Net Worth $5 Million
Source Of Income Mathematician
House Living in own house.
Donald Knuth is one of the richest Mathematician from United States. According to our analysis, Wikipedia, Forbes & Business Insider, Donald Knuth 's net worth $5 Million. (Last Update: December 11, 2023)
![[dubious text from "Celebrity Birthdays" site.]
Height, Weight & Body Measurements
Donald Knuth height Not available right now. Donald weight Not Known & body measurements will update soon.
Who is Donald Knuth Dating?
According to our records, Donald Knuth is possibily single & has not been previously engaged. As of December 1, 2023, Donald Knuth’s is not dating anyone.
Relationships Record : We have no records of past relationships for Donald Knuth. You may help us to build the dating records for Donald Knuth!](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:t7ajsa37yphkf2vp6ydd3mvk/bafkreieaj4jf63ljkxnftog7ojp6y4ekxgf7p6nbdyoclam7nfxw5d5zgm@jpeg)
[dubious text from "Celebrity Birthdays" site.]
Height, Weight & Body Measurements
Donald Knuth height Not available right now. Donald weight Not Known & body measurements will update soon.
Who is Donald Knuth Dating?
According to our records, Donald Knuth is possibily single & has not been previously engaged. As of December 1, 2023, Donald Knuth’s is not dating anyone.
Relationships Record : We have no records of past relationships for Donald Knuth. You may help us to build the dating records for Donald Knuth!
Somehow ended up clicking to the "Donald Knuth" page on "Celebrity Birthdays", and I wonder how these things are generated.
03.05.2025 06:07 — 👍 1 🔁 0 💬 0 📌 0
Original post on mathstodon.xyz
@zachweinersmith.bsky.social Have you run into the work of Lenore & Manuel Blum (https://arxiv.org/abs/2403.17101)? I first heard Manuel Blum speak about his consciousness project some 20+ years ago, and he argued precisely that the perspective of theoretical computer science could bring […]
14.04.2025 11:39 — 👍 1 🔁 0 💬 0 📌 0
I gave a tutorial talk today about "(generalized) fibrations for logic, automata and language theory", mainly focused on the automata part. Slides if you are interested: https://noamz.org/talks/dagstuhl.tutorial.2025.04.02.pdf
02.04.2025 16:27 — 👍 0 🔁 1 💬 0 📌 0
Original post on mathstodon.xyz
just read Oleg Kiselyov's blog post "do-while loops have always been in OCaml" (https://okmij.org/ftp/ML/index.html#do-while), and laughed out loud when I got to the punchline. I haven't done any OCaml programming in a long time but it makes me want to try it again, surely a beautiful language […]
03.03.2025 16:18 — 👍 10 🔁 4 💬 1 📌 0
@johncarlosbaez Gödel's first and second?
28.02.2025 05:32 — 👍 0 🔁 0 💬 1 📌 0
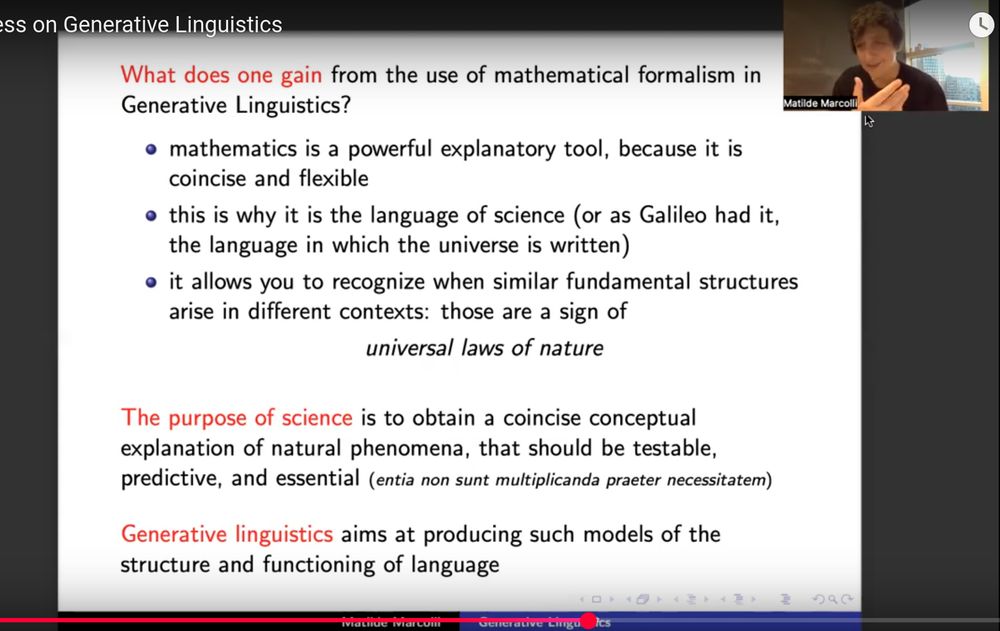
slide from Matilde Marcolli talk
What does one gain from the use of mathematical formalism in Generative Linguistics?
* mathematics is a powerful explanatory tool, because it is concise and flexible
* this is why it is the language of science (or as Galileo had it, the language in which the universe is written)
* it allows you to recognize when similar fundamental structures arise in different contexts: those are a sign of _universal laws of nature_
The purpose of science is to obtain a concise conceptual explanation of natural phenomena, that should be testable, predictive, and essential (entia non sunt multiplicanda praeter necessitatem)
Generative linguistics aims at producing such models of the structure and functioning of language

slide from talk by Matilde Marcolli, title: "Where is the explanatory power? Where is the understanding?"
* do LLMs disprove Generative Linguistics, as some claim?
... No: quite the opposite, as the generative process of syntax is robust enough to emerge in keys and queries from a probabilistic smear of semantic relatedness
* do LLMs dispense with the need for theoretical linguistics?
... No: successes of LLMs as language-handling machines do not provide us with a fundamental, coincise, explanatory, conceptual understanding of the structure of language
* can LLMs be useful to theoretical linguistics?
.... Possibly, as an experimental apparatus for the investigation of inverse problems in the syntax-semantics interface
* if we have a functioning technology, do we need science?
I really enjoyed this "Public Address on Generative Linguistics" by Matilde Marcolli:
https://www.youtube.com/watch?v=-gx3SK7FvKk
Marcolli is a mathematical physicist and recent [!] collaborator of Noam Chomsky. This lecture from Oct 2023 is broadly about […]
[Original post on mathstodon.xyz]
20.12.2024 17:01 — 👍 3 🔁 1 💬 0 📌 0

I'm pleased to announce that the Heyting Day will be held in Amsterdam on Friday 14 March 2025.
Its theme will be models of #intuitionism and #computability and mark the retirement of Jaap van Oosten.
The invited speakers are:
- @andrejbauer (Ljubljana)
- […]
[Original post on mathstodon.xyz]
20.12.2024 08:34 — 👍 2 🔁 4 💬 1 📌 0
@julesh *probably* a coincidence but this image reminds me a lot of the passageway to the bathrooms at the entrance to the research section of the Bibliothèque Nationale de France (https://www.bnf.fr/sites/default/files/styles/carousel_lg/public/2019-02/BNF_2011_055254.jpg).
15.12.2024 21:44 — 👍 0 🔁 1 💬 1 📌 0




![[dubious text from "Celebrity Birthdays" site.]
Donald Knuth is one of the most popular and richest Mathematician who was born on January 10, 1938 in Wisconsin, Wisconsin, United States. Mathematician and engineer who was arguably most recognized as the Professor Emeritus at Stanford in Palo Alto, California.
Henry Suzzallo once studied at Stanford University, where he served as the Professor Emeritus.](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:t7ajsa37yphkf2vp6ydd3mvk/bafkreig4r4kvrmmnnyb5cxnwgbu3hfszwnqf5m2olopjp4w5vryxhhixem@jpeg)
![[dubious text from "Celebrity Birthdays" site.]
Donald Knuth Net Worth
Net Worth $5 Million
Source Of Income Mathematician
House Living in own house.
Donald Knuth is one of the richest Mathematician from United States. According to our analysis, Wikipedia, Forbes & Business Insider, Donald Knuth 's net worth $5 Million. (Last Update: December 11, 2023)](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:t7ajsa37yphkf2vp6ydd3mvk/bafkreih37wldurjtgripjrreb7gfzy7hbde7xme6cegdeiwtov3wdoiz34@jpeg)
![[dubious text from "Celebrity Birthdays" site.]
Height, Weight & Body Measurements
Donald Knuth height Not available right now. Donald weight Not Known & body measurements will update soon.
Who is Donald Knuth Dating?
According to our records, Donald Knuth is possibily single & has not been previously engaged. As of December 1, 2023, Donald Knuth’s is not dating anyone.
Relationships Record : We have no records of past relationships for Donald Knuth. You may help us to build the dating records for Donald Knuth!](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:t7ajsa37yphkf2vp6ydd3mvk/bafkreieaj4jf63ljkxnftog7ojp6y4ekxgf7p6nbdyoclam7nfxw5d5zgm@jpeg)


