Viktor Blåsjö

YouTube video by 3Blue1Brown Why ruler and compass? | Guest video by ⁨@bensyversen⁩

Much of Euclid’s Elements is easily misunderstood. Some proofs seem to have logical gaps. Some constructions seem pointless, others seem needlessly convoluted.

Each of these provides a window into how the ancient Greeks thought about math and the philosophical role that geometry played.

the Notices of the DEI

I believe the Greek says straight lines (εὐθεῖας γραμμὰς) just as in the Elements. "Rays" seems to be an erroneous and misleading translation.

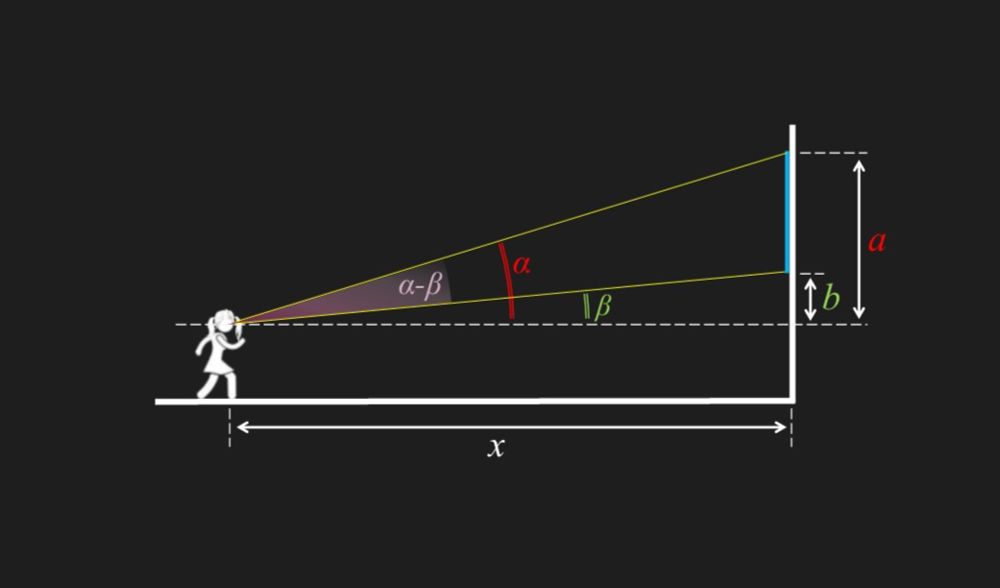
Optimal Picture Viewing Distance

Euclid says correctly: If one draws such lines, this is how they behave. For example when doing problems like this: datagenetics.com/blog/decembe... Everything about this perfectly fits Euclid's text.

A true statement about how lines emanating from a point behave. It does not say that that is how human vision actually operates physically. We use the same principle today when doing geometrical optics: connect the eye to points of interest by lines, then investigate the angles between them etc.

Nothing in Euclid says that he was committed to an extramission theory of sight. He describes visual phenomena relative to an observer, but this could just as well be understood the same way as when a heliocentric astronomer uses a geocentric framing or terminology for practical purposes.

In my geometry course I made a slide on this inspired by your book. intellectualmathematics.com/geometry/

Not sure, maybe eventually but I have other things planned there to appear soon.

There is no Euclidean proof of the fourth postulate Gil-Férez et al. (2025) claim to prove Euclid's fourth postulate by strictly Euclidean means. In fact, however, they assume a principle that is neithe…

My new article, on why Euclid had to postulate that all right angles are equal: www.sciencedirect.com/science/arti...

There is hardly anything substantial as far as I know, except old things in Italian. On a later part of the abacus school tradition I enjoyed the chapter zbmath.org/7940758 and hope to read the book link.springer.com/book/10.1007....

Viktor Blåsjö's review of the book "Form & Number: A History of Mathematical Beauty" by Alan J. Cain, is now live at tug.org/books/review...

What is mathematical beauty? tug.org/books/review...

My obituary of Henk Bos, who opened the eyes of so many of us to the history of mathematics: research-portal.uu.nl/ws/portalfil...

But how are you supposed to “draw the tangent line”? Archimedes doesn’t say. Does he think that drawing tangents is somehow “more given” or more basic than rectifying a circle (i.e., knowing π)? Unclear why one would think that.

I believe Aristarchus did not make a "lousy measurement" (15:58). Rather, he deliberately underestimated the size of the sun, and showed that even in this worst-case scenario it is way bigger than the earth (i.e. heliocentrism wins). See arxiv.org/abs/2102.06595 §7.6.

Torricelli's trumpet is not counterintuitive Opinionated History of Mathematics > • Play There is nothing counterintuitive about an infinite shape with finite volume, contrary to the common propaganda version of the calculus trope known as Torricelli's trumpet. Nor was this result seen as counterintuitive at the time of its discovery in the 17th century, contrary to many commonplace historical narratives. Transcript Torricelli's trumpet is not counterintuitive. Your calculus textbook lied to you. You've probably heard of this cliché…

I like this rant: I never found Gabriel's horn / Torricelli's trumpet to contradict my intuition, though it's a fun example. https://intellectualmathematics.com/blog/torricellis-trumpet-is-not-counterintuitive/

Torricelli’s trumpet is not counterintuitive There is nothing counterintuitive about an infinite shape with finite volume, contrary to the common propaganda version of the calculus trope known as Torricelli’s trumpet. Nor was this result seen as...

ICYMI there's a new episode of @viktorblasjo.bsky.social's podcast out this week, first new episode in over a year. A fun listen as always

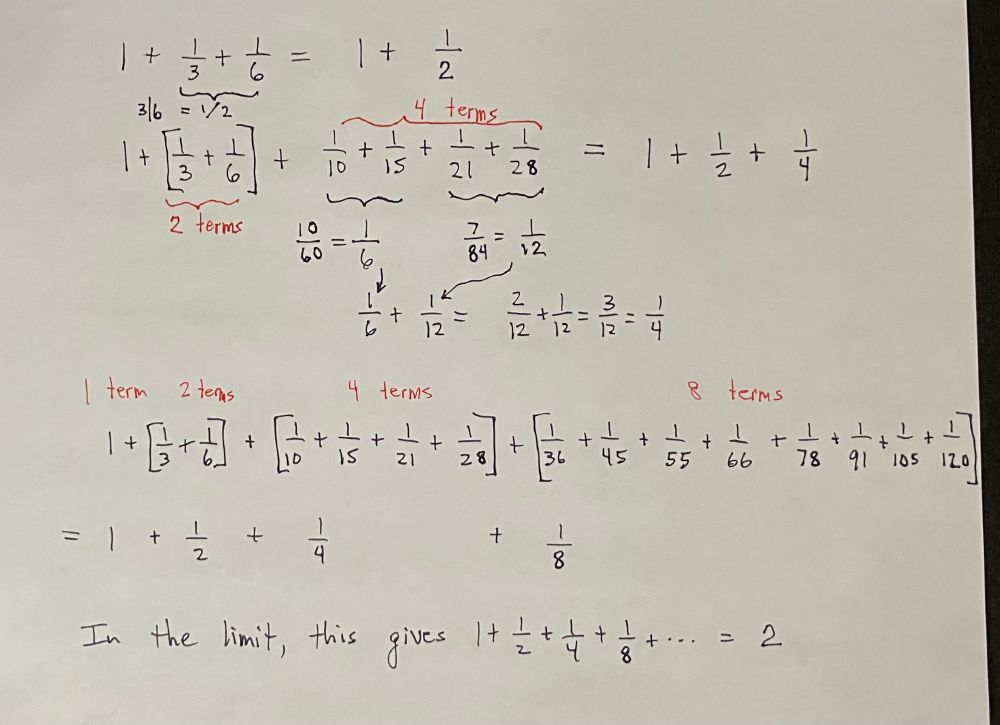
Today I learned (ht Viktor Blasjo) how Huygens summed the reciprocals of the triangular numbers. He regrouped the series and showed that it equals the geometric series 1+1/2+1/4+... = 2, like so!

Sometimes 1 30 was written "1 and ½" to emphasise that 1½ was meant, not 90. Another method of disambiguation was by the size of the characters: a 1 written bigger represents 60, etc. See Neugebauer, Exact sciences in antiquity, pp. 19-20.

New Medieval Books: The Optics of Ibn al-Haytham Books IV-V - Medievalists.net A translation of a section from Ḥasan Ibn al-Haytham's work, Book of Optics, which was written between 1011 and 1021. It is a major work of scientific history, changing the way people understood eyesi...

New Medieval Books: The Optics of Ibn al-Haytham Books IV-V www.medievalists.net/2024/08/new-... #books

Mathematical Rigour and Informal Proof Cambridge Core - Philosophy of Science - Mathematical Rigour and Informal Proof

My book in the Cambridge Elements series on "Mathematical Rigour and Informal Proof" is out today! It's free to download for two weeks, so please share it widely with anyone who may be interested. 🥳🎉
www.cambridge.org/core/element...

🥁: Historian of mathematics, famous contrarian and "Intellectual Mathematics" podcaster @viktorblasjo.bsky.social is now on Bluesky! #histsci