David R. Agrawal

Online Spatial & Urban Seminar Registration: To receive the Zoom link for the seminars please register on the Zoom webinar page. If you have participated in the last two seasons of the OSUS seminar, you do not need to register…

📣 Today! Join us @osus-info.bsky.social at 11:30 ET, 4:30 pm (UK), or 5:30 pm (Euro)!

David Agrawal (UC Irvine) presents “Policy Competition in a Spatial Economy” (osus.info)

Hosted by @urbaneconomics.bsky.social

Looking forward to presenting this new paper on the welfare effects of policy competition in the OSUS seminar.

Paper: papers.ssrn.com/sol3/papers....

Get the zoom link for the talk here: us06web.zoom.us/webinar/regi...

An early Christmas gift 👇

Thanks, @davidragrawal.bsky.social, Jim Poterba and @omzidar.bsky.social, for leading this project so successfully.

It was an honor and a pleasure to contribute a chapter on corporate tax competition among the Swiss cantons.

Thanks to our editor at @uchicagopress.bsky.social
and all the authors who contributed @jeffreypclemens.bsky.social @stanveuger.bsky.social @s-stantcheva.bsky.social @mariusbrulhart.bsky.social @kurtschmidheiny.bsky.social & many others not on here!

Excited to receive our new 536 page book on tax competition and coordination in the mail today:

"Policy Responses to Tax Competition" (w/ Poterba &
@omzidar.bsky.social)

I know everyone is looking forward to order it here:
amazon.com/-/es/Respons...

Theoretical Economics Volume 20, Issue 3 (July 2025) is now online econtheory.org

Last day to submit! Looking forward to seeing you in Berlin!

Local Public Finance and Fiscal Federalism Around the World The aim of this conference is to bring together international scholars of all career stages working on topics of local public finance, fiscal federalism, interjurisdictional competition and cooperatio...

🚨 1 week left! 🚨
Working on local public finance or fiscal federalism?
Present your research in Berlin 🇩🇪
📅 July 7–8, 2025
📍 Harnack-Haus
🎙️ Keynote: @davidragrawal.bsky.social (UC Irvine)
✈️ Travel & stay covered
📩 Apply by April 15 → events.tax.mpg.de/event/10/
Please share this! ♻️

Local public economics and federalism are important!

I'm excited to return to Berlin to give the keynote at this conference on local public finance issues around the world.

Travel funding available!

Submit your local PF papers here:
events.tax.mpg.de/event/10/

Excited to serve another term as Editor-in-chief of @itaxjournal.bsky.social with this new fantastic team!

Thanks to both Ron and Nadine for their service to the public finance community, especially during the crazy pandemic years. I learned a lot & enjoyed working with them over the last four years where submissions to the journal almost doubled!

And follow @itaxjournal.bsky.social which is new here!

Elasticities are endogenous and government choices. Eg they can be influenced by sale or things like zoning. We wanted to add this to the model but will save for future work

An interesting question is where the optimal borders are in light of this heterogeneity

Thanks! Can you say more about the model application with SALT?

This is really cool! Have always thought this was a missing extension, particularly in the SALT context

Check out the paper here:
econtheory.org/ojs/index.ph...

We are grateful to @florianscheuer.bsky.social for his extensive comments as editor and for the three excellent referees he selected, especially Referee B whose reports were some of the most insightful I have ever seen.

Highly recommend the process at
@econtheory.bsky.social

In ongoing work, we verify our theoretical commodity tax result empirically. That paper is coming soon!

Finally, we discussion how our results might be applicable to spatial price competition with multiple firms, to spatial voting models, or to border effects in trade.

Capital competition models with two jurisdictions place assumptions on moving costs.

With three jurisdictions, the distribution of moving costs for firms plays the same role as population density.

Again bigger jurisdiction can set lower rates!

Profit shifting models often have 2 jurisdictions and quadratic costs.

We generalize to three jurisdictions with a more general convex cost function for profit shifting.

The higher derivatives of the cost function play the same role as population density.

Finally, we show the result generalizes beyond spatial commodity tax competition to models of profit taxation (Keen and Konrad ) or capital taxation (Mongrain and
Wilson).

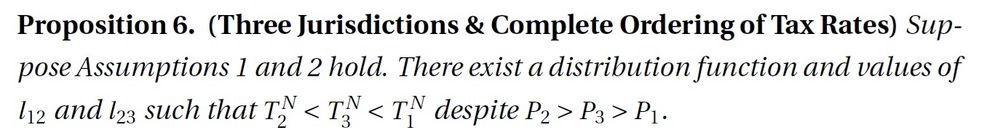
And we go even further to show there exist a distribution function and jurisdiction boundaries such that the complete ordering of tax rates reverses from the rankings of populations.

In other words, the denominators of the optimal tax rates are now different!

Classic result can be overturned b/c with 3 jurisdictions, a jurisdiction can attract cross-border shoppers from 2—instead of 1 jurisdiction

Thus, tax base sensitivities are no longer equal

Elasticities in Ramsey rule depend on size and on the average base change at 2 borders!

We conclude that we can find a population jurisdiction with three jurisdictions such that P1 > P2 and T1 < T2.

That is, a smaller jurisdiction can set a higher
tax rate than the next largest jurisdiction.

Then show if the border between 1/2 makes 1 smaller, T1 - T2 is decreasing.

Thus, reduce this border a small amount such that
T1 < T2 > T3

But under the perturbed population distribution we have P1 > P2 > P3.

QED (many complex details in paper)

Small perturbation results in P1 > P2 > P3

Although the initial equilibrium satisfied the assumptions for existence, the perturbed density may not.

But we prove the equilibrium of the original unperturbed game is also an equilibrium to a perturbed game! T1 = T2 > T3

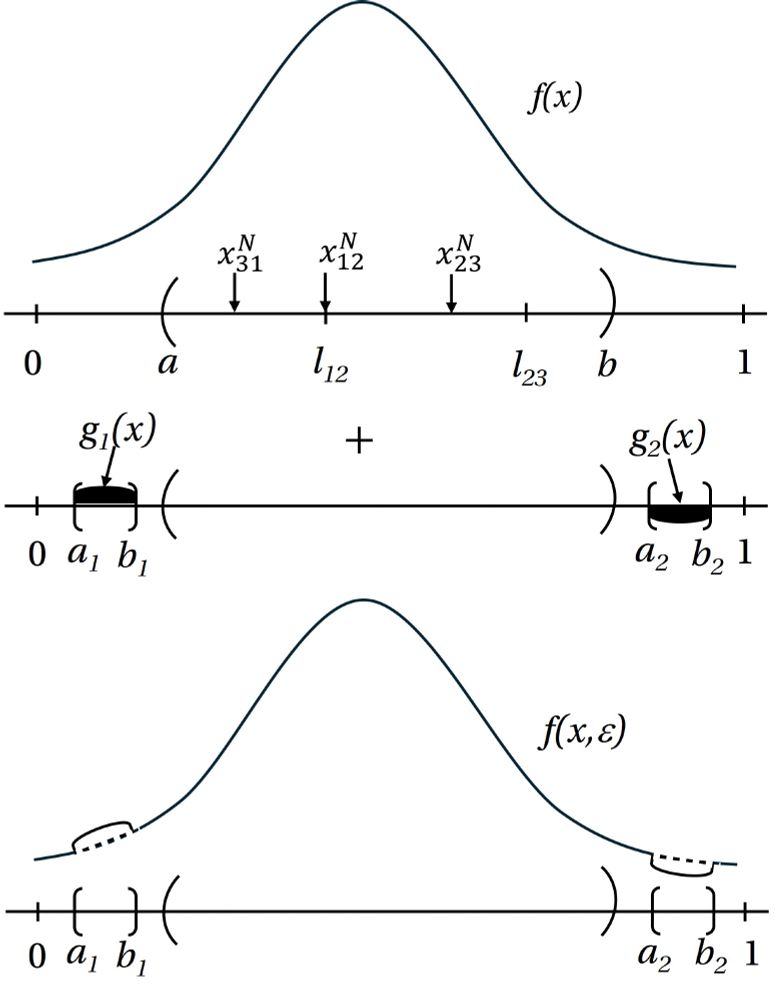
Finally, we generalize this result for an arbitrary f(x) and asymmetric jurisdictions.

Proof strategy:

Start from a Nash eq where population P1 = P2 > P3 and taxes are T1 = T2 > T3

Make a specific population perturbation that changes populations but leaves tax bases unchanged

We first prove smaller places set higher rates using a simple example:

Population distribution is triangular.

2 jurisdictions are symmetric and have a common border at the lowest density point.

Then for a certain range of their lengths, we get

little t > big T despite p < P

First we need to show an equilibrium exists and is unique.

If f(x) is log-concave and satisfies one other mild condition, then the game is supermodular and existence follows.