Toru3

リーマン積分が上手くいかない簡単な例だと有理数だと1で無理数だと0という関数を積分するとか

ドミニオンの結果

dominionの結果

東北大テニュア(テニュアではない)の話?

久しぶりにサイゼリヤに行ったのだが、ラムの串焼き(商品名は確か違うけど)が美味しかった。あと、水牛のチーズも良かった。

腹減った(この後健康診断がある)

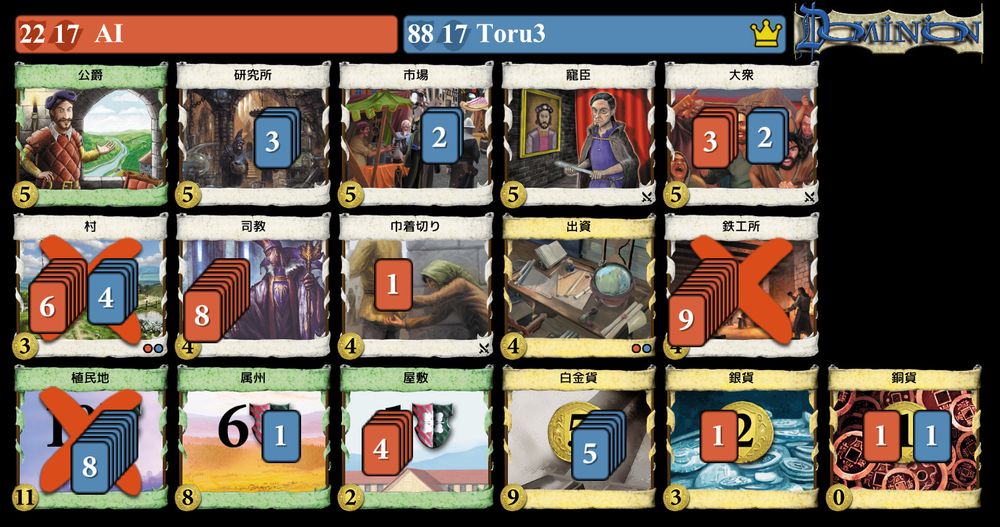
88 vs 22

#ドミニオン

これは本当にそう。勝ち負けではなく、1人では得られないより良い結論(アウフヘーベン)を得るためにやるという意識が必要。

議論は論破しようという気持ちでするなと子には伝えている

Twitter君の調子が悪そう

組版に「正解」はあるの？ 新潮社に学ぶ、良い組版の考え方｜モリサワ　note編集部 組版を学ぶ人が陥りがちな「選択肢がたくさんあるけど、結局何を使うのが正解なの……？」という疑問。 その疑問を解決するために、日本を代表する出版社の1つであり創業100年以上の歴史を持つ新潮社様にお話を伺いました。 詳しい経緯は前回記事をチェック！ 新潮社様にお伺いしました お話を伺った方 金川 功 （かながわ いさお）さん 営業部 元デジタル編集支援室長として、新潮社の書籍のDTP組版の実践と...

いい話！

あけましておめでとうございます
今年もよろしくお願いします

ターミナルを使いこなそう 〜 Vimはいいぞ！ゴリラと学ぶVim講座(5) | さくらのナレッジ こんにちは。 ゴリラ.vimを運営しているゴリラです。 前回の記事では、コマンドラインモードについて解説しました。:%!jq でテキストを整形したりと外部コマンド連携が得意なモードではありますが、コマンドの実行が完了する […]

knowledge.sakura.ad.jp/23018/

いや違うな:terminal

vimshellがそれっぽい

rlwrap?

有限次元だと実はどのノルムでも収束性は変わらないけど、無限次元だと変わってきたり、有限次元だと座標の各成分が収束すれば収束するけど無限次元だと各成分が収束しても収束しない場合がある。

無限次元空間も中々

非可算無限、キモい

そういえば今日は久しぶりにマクドナルドに行ってダブチを食べてきた

投票done

これは趣味でOSSにPR出すときの話

やはり怒り駆動開発というか、不満があった時に勢いで直すPR作るのが一番PR作りやすい気がする。

そういえばモバイルSuicaは電池切れても使えると聞いたので、試してみたらちゃんと使えた

完備の話? 考えられるけど命題2.4とかは成り立たなくなる。
Zだと稠密じゃないのでQにすると(1, √2) \cap Qは開集合となる。ここで、Q \ (1, √2)=((-∞, 1] \cup [√2, ∞)) cap Qは命題2.4より閉集合となるはずだが、Q \ (1, √2)からなる数列で√2に収束する列が存在する一方、√2 ∉ Q \ (1, √2) より閉集合でない。

ただの距離空間じゃなくて完備距離空間かな。収束先が無いと困りそうだから

距離空間を前提にするならその定義でも同値になるはず。同値な定義が色々ある中でそれを採用した理由までは分からない。（対称性がなくて気持ち悪いのはまあそうね）

ja.m.wikipedia.org/wiki/%E9%96%...

R上だと空集合とRは開集合かつ閉集合だよ。

位相の定義は開集合系でやるのがメジャーだと思うけど、閉集合系や近傍系とかでも同値な定義が出来る。