Aditya Makkar

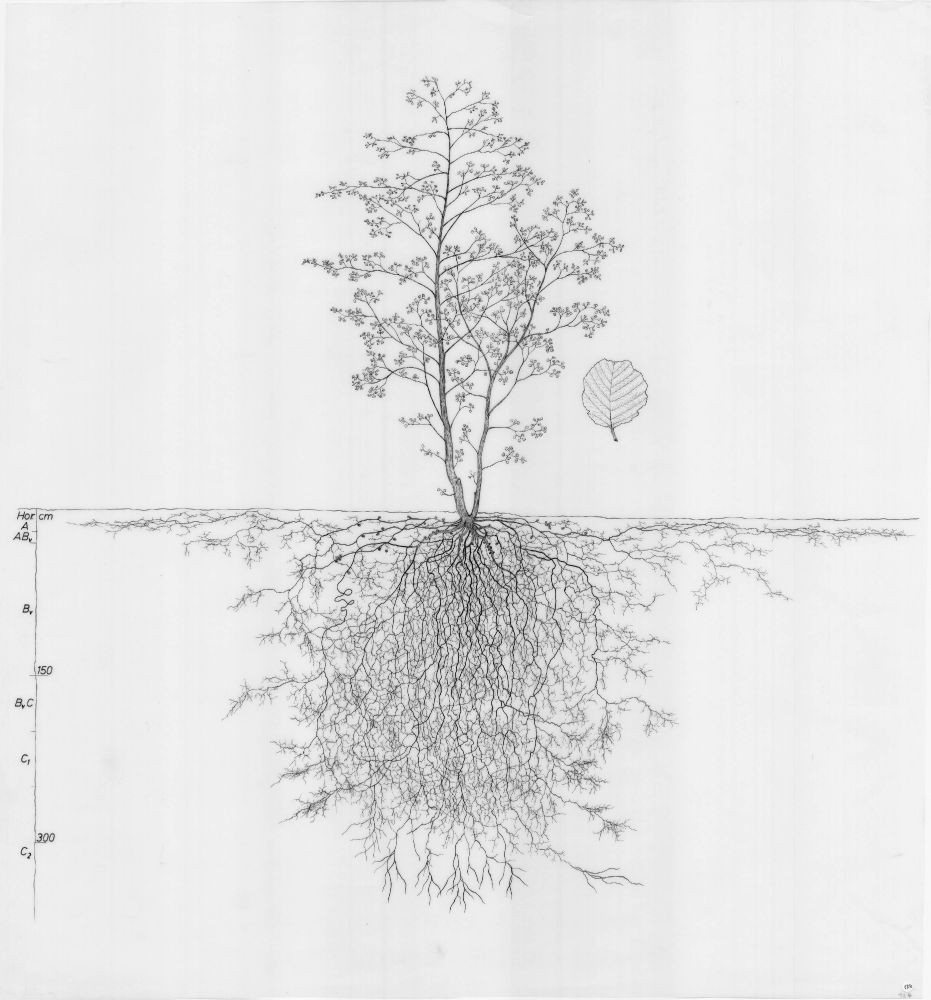
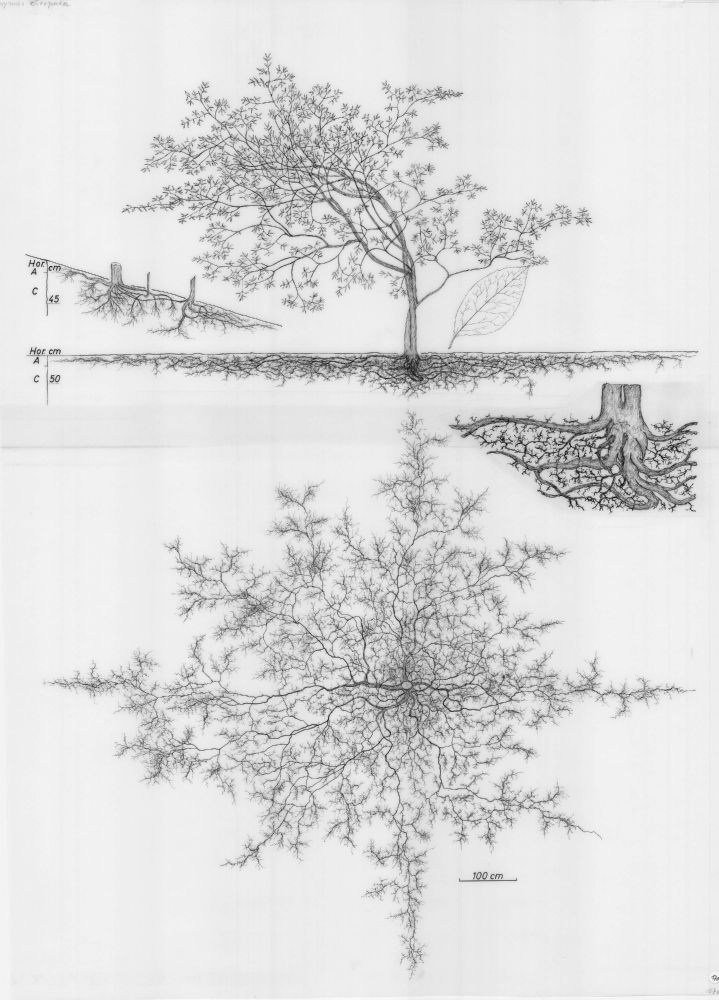
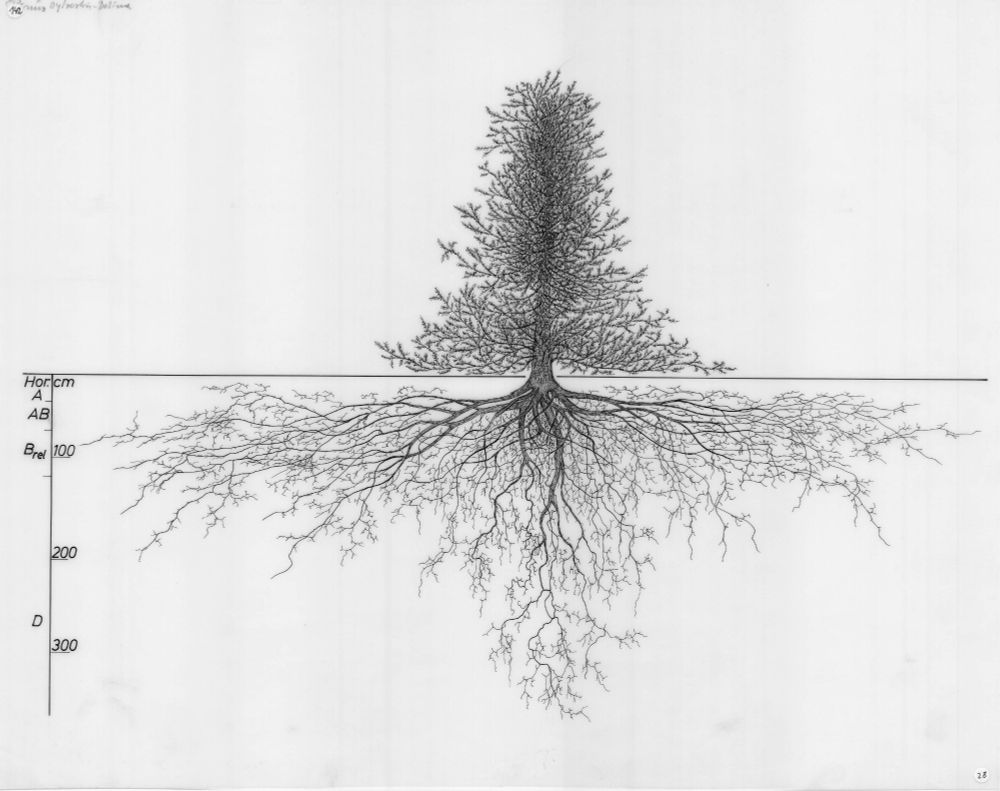
Mesmerizing
Source: images.wur.nl/digital/coll...

Supertzar, or the Hand of Doom The sleep of reason produces utility monsters.

A critical look at intelligence explosion arguments, with references to I.J. Good, Jimmy Savage's small and large worlds, Kathleen Wilkes' argument against thought experiments in psychology, and Tolkien's theory of subcreation (+ some Sabbath references): realizable.substack.com/p/supertzar-...

Quanta has some coverage on her solution, including from this colourful presentation. One detail that i liked -- she had worked through advanced undergrad math curriculum by herself by 14. Hopefully she is able to handle the sudden attention well.

www.quantamagazine.org/at-17-hannah...

Great intro to Optimal Stopping on those lecture notes by Thomas S. Ferguson

www.math.ucla.edu/~tom/Stoppin...

The Power of Resets in Online Reinforcement Learning Simulators are a pervasive tool in reinforcement learning, but most existing algorithms cannot efficiently exploit simulator access -- particularly in high-dimensional domains that require general fun...

This week's #PaperILike is "The Power of Resets in Online Reinforcement Learning" (Mhammedi et al., 2024).

If you're doing RL in sim, why not use the sim to its full potential? Reset to any state! (gym.Env.reset() is not all we need.)

PDF: arxiv.org/abs/2404.15417

my p doom? sorry that's not a valid sigma algebra

Gaussian Processes and Reproducing Kernels: Connections and Equivalences This monograph studies the relations between two approaches using positive definite kernels: probabilistic methods using Gaussian processes, and non-probabilistic methods using reproducing kernel Hilb...

Looks like a great new foundations and trends monograph arxiv.org/abs/2506.17366

Born on 23 June 1912 in London, Alan Turing, a mathematician, cryptographer and a pioneer in computer science and artificial intelligence

pubs.aip.org/physicstoday...

Robust Autonomy Emerges from Self-Play Self-play has powered breakthroughs in two-player and multi-player games. Here we show that self-play is a surprisingly effective strategy in another domain. We show that robust and naturalistic drivi...

Hiring a postdoc to scale up and deploy RL-based planning onto some self-driving cars! We'll be building on arxiv.org/abs/2502.03349 and learn what the limits and challenges of RL planning are. Shoot me a message if interested and help spread the word please!

Full posting to come in a bit.

It was a dream come true to teach the course I wish existed at the start of my PhD. We built up the algorithmic foundations of modern-day RL, imitation learning, and RLHF, going deeper than the usual "grab bag of tricks". All 25 lectures + 150 pages of notes are now public!

Does everyone in your community agree on some folk knowledge that isn’t published anywhere? Put it in a paper! It’s a pretty valuable contribution

—I want a painting of a solar eclipse. Have you seen one?
—You bet!

Yeah they’re getting quite good. I think the model I have is something like “clever but sort of dishonest undergrad with an encyclopedic but idiosyncratic knowledge of the arxiv.” “Prove [well-known result with a short-ish proof]” is well within their capabilities though they do sometimes screw up.

If the last time you tried to use an LLM for math was ~4 or 5 months ago it’s worth firing up Gemini 2.5 (which you can try for free) or ChatGPT o3 and getting a sense of how rapidly things have progressed.

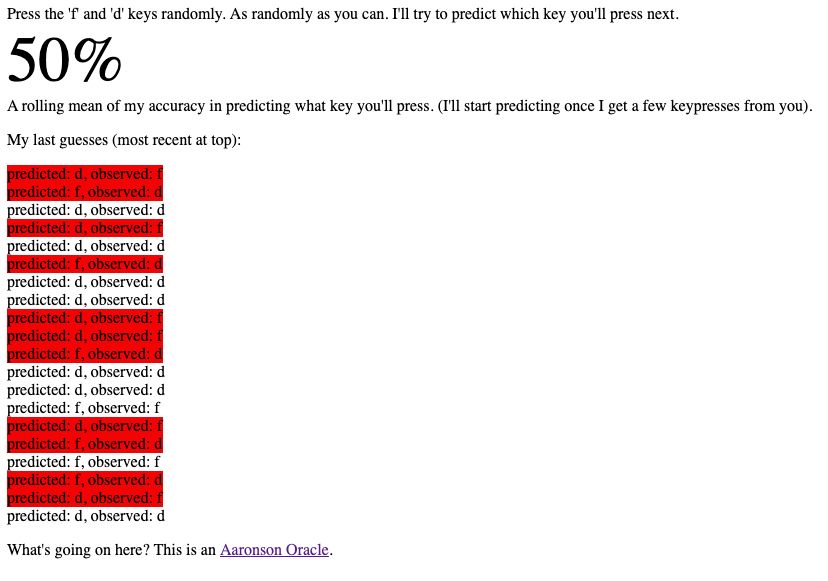
crushing it on the free will machine (people.ischool.berkeley.edu/~nick/aarons...)

GitHub - TikhonJelvis/RL-book Contribute to TikhonJelvis/RL-book development by creating an account on GitHub.

I have learnt good practices from your code for the RL book. It's very close to what I do daily.
github.com/TikhonJelvis...

How does one learn to write good code?

NYU Tandon receives Google DeepMind grant to advance AI adaptation | NYU Tandon School of Engineering

A cute lil writeup of our work trying to scale up meta-learning for partner adaptation:
engineering.nyu.edu/news/nyu-tan...

Also, my first grant!

The Stone-Weierstrass theorem states that any continuous function on a compact Hausdorff space can be uniformly approximated by elements of a subalgebra, provided the subalgebra separates points and contains constants. buff.ly/MbZOAG0

Comprehensive presentation of the "Theorem of the Day", starting with a statement of this theorem. Kuratowski’s 14-Set Theorem : Let T = (S, T ) be a topological space and for any subset X of S, denote by C(X) the complement S \X of X, and by K(X) the topological closure of X. Starting with an arbitrary subset of S , apply C and K repeatedly in any order; then the number of different sets that may be produced is at most 14.

Theorem of the Day (April 28, 2025) : Kuratowski’s 14-Set Theorem
Source : Theorem of the Day / Robin Whitty
pdf : buff.ly/ZKGM3fm
notes : buff.ly/A2DK4wC
#mathematics #maths #math #theorem

I like papers that have such intros. From the snippet you wouldn't guess (unless you already have the background) what [application] the paper is about. arxiv.org/abs/2504.16349

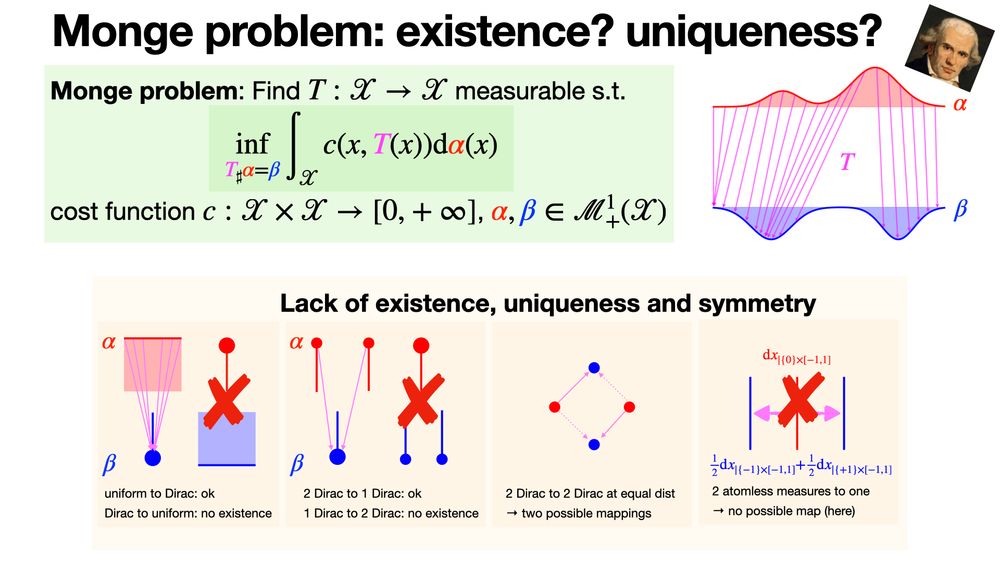
A Monge map, i.e., a solution to optimal transport Monge problems, may not always exist, be unique, or be symmetric with respect to the source and target distributions. It was one of the motivation to introduce Kantorovich relaxation. math.univ-lyon1.fr/~santambrogi...

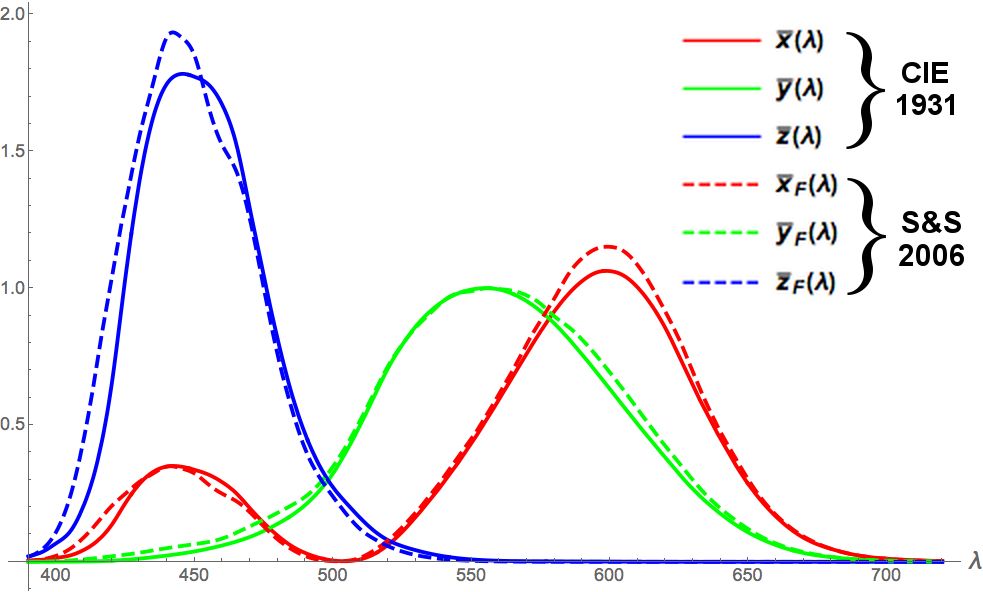
Source: https://commons.wikimedia.org/wiki/File:XYZ_color_matching_functions,_CIE_1931_and_Stockman_%26_Sharpe_2006.jpg

Colours correspond to infinite-dimensional vectors, since there are infinitely many wavelengths of light.

But humans can only perceive a three-dimensional projection of colour (red, green, & blue).

What's interesting is that it's *not* an orthogonal projection. Here's a plot of the basis vectors.

I hope someone writes a Notices article in the next edition, like the one that Stroock wrote for Malliavin www.ams.org/notices/2011...

Hardy showed in 1916 that the last two unnatural looking conditions can be replaced with ab ≥ 1.

www.ams.org/journals/tra...

Statistical Optimal Transport This monograph aims to offer a concise introduction to optimal transport, quickly transitioning to its applications in statistics and machine learning.

PSA — if you’re interested in learning about statistical aspects of optimal transport, check out this new monograph by Sinho Chewi, Jonathan Niles-Weed, and Philippe Rigollet: link.springer.com/book/10.1007...

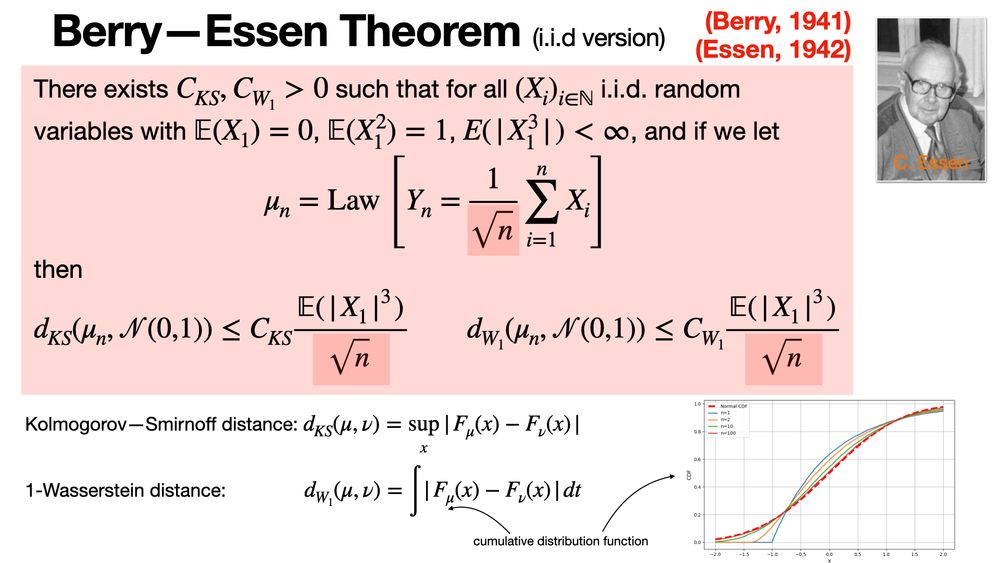
The Berry-Esseen theorem quantifies how fast the distribution of the sum of independent random variables converges to a normal distribution, as described by the Central Limit Theorem (CLT). It provides an upper bound depending on skewness and sample size. terrytao.wordpress.com/2010/01/05/2...

The workshop list is one of those things that makes clear why RLC is so good. I can't choose which one I'd want to attend!

Today, I'm revisiting (some slides which I made for) a short course which I gave in December on "Geometric Functional Inequalities for Markov Chains", and I'm thinking about other ways of motivating the study of this topic. I want to have a go at re-motivating it, from scratch:

Maxim Raginsky: Stochastic Differential Equations in Optimization, Learning, and Control, A Brief History of Ideas Zoom Recording ID: 9738665007 UUID: qR9vrIQ8SqS0qmVwqpi4pw== Meeting Time: 2023-01-12 11:17:42pmGMT

Two years ago I taught a course on SDEs in control, optimization, and learning. The introductory lecture can be watched here (I didn’t record anything else, used the blackboard for the rest of the semester): mediaspace.illinois.edu/media/t/1_1d...