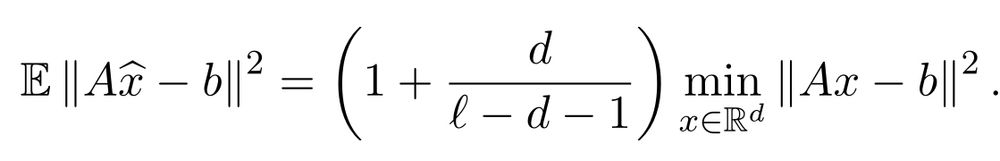Ethan Epperly

Gaussian integration by parts. Let z be a standard Gaussian random variable. Then E[zf(z)] = E[f'(z)].

New blog post up about the amazingly useful Gaussian integration by parts formula! As an application, we use it to analyze power iteration from a random start www.ethanepperly.com/index.php/20...

2025 July Prize Spotlight | SIAM Congratulations to the SIAM prize recipients who will be recognized at AN25, ACDA25, CT25, and GD25!

Very excited to share that I’ve been awarded a SIAM student paper prize! I look forward to seeing any of you who will be at #SIAMAN25 in Montréal. Thanks to the committee for selecting me for this honor www.siam.org/publications...

Reflections on five years of blogging www.ethanepperly.com/index.php/20...

Also, if you never want to miss a blog post, you can sign up to receive email notifications here! eepurl.com/i5M2P2

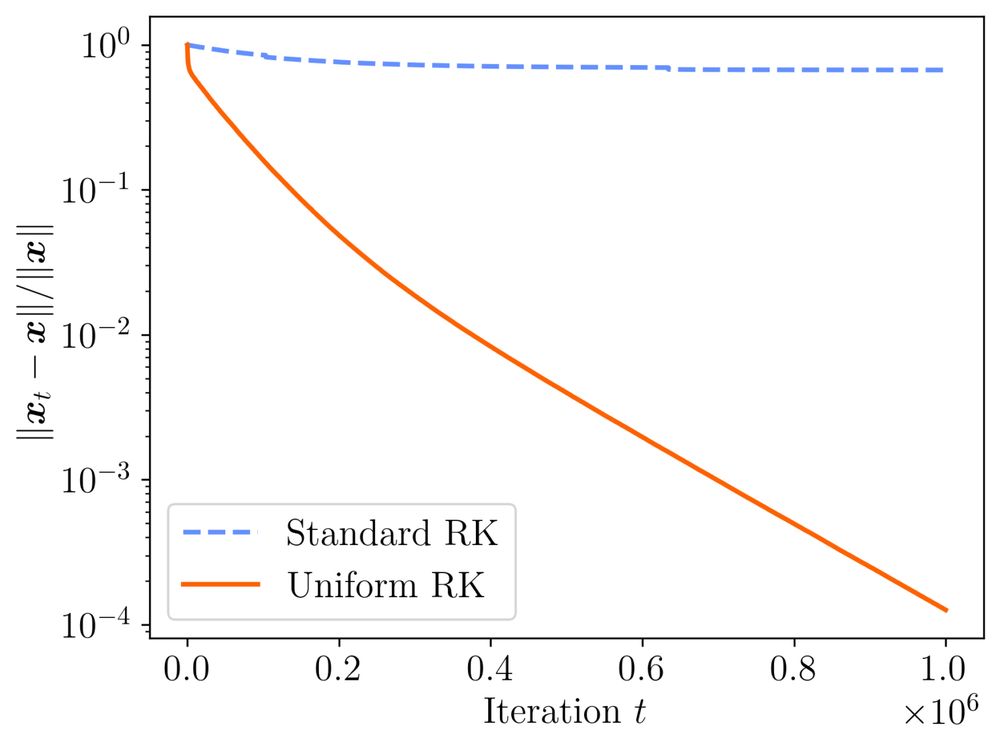
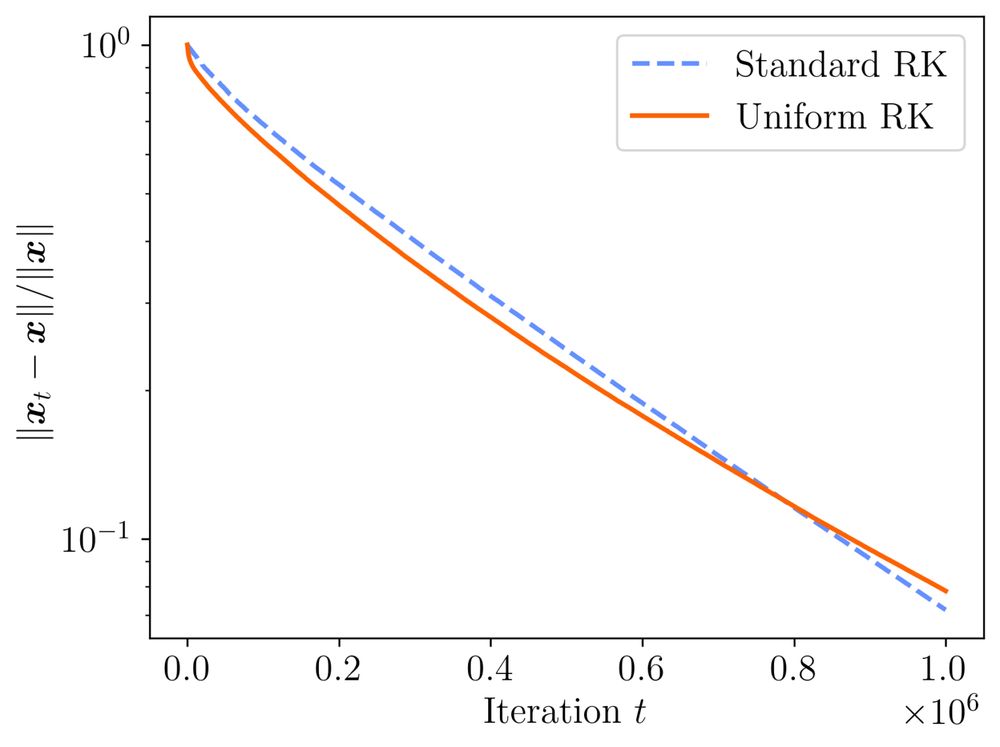
New blog post up about the randomized Kaczmarz algorithm. The classic RK algorithms samples rows according to their squared norms, but what happens if you sample them uniformly? The answer surprised me: Uniform sampling is often just as good or even better www.ethanepperly.com/index.php/20...

New blog post out about the new Polar Express algorithm of Amsel, Persson, Musco, and Gower for computing the matrix sign function with applications to the Muon optimizer www.ethanepperly.com/index.php/20...

New blog post out in my series on Markov chains! In this post, I discuss Poincaré inequalities and their connection to mixing of Markov chains www.ethanepperly.com/index.php/20...

a bunch of red and white balls in the sky Alt: A lot of red and white Pokeballs falling from the sky

🧩 New week, time for our weₐᵉkly quiz! Today, another thing a bit random: Pokémon! Ash and Barry want to catch 'em all: all of them. You know, Pikachu, Jigglypuff, err... Charmander? It's been a while.

So, n Pokémon to catch, and no idea how long it'll take. Gotta help them out! #WeaeklyQuiz

1/

We start by computing $x^\top (A\circ M)x$: $$x^\top (A\circ M)x = \sum_{i,j=1}^n x_i (A\circ M)_{ij} x_j = \sum_{i,j=1}^n x_i A_{ij} M_{ij} x_j.$$Now, we may rearrange the sum, use symmetry of $M$, and repackage it as a trace $$x^\top (A\circ M)x = \sum_{i,j=1}^n x_i A_{ij} x_j M_{ji} = \tr(\operatorname{diag}(x) A \operatorname{diag}(x) M).$$This the trace formula for quadratic forms in the Schur product.

Ack! Typesetting glitch. It was meant to be diag(x) A diag(x) M

Proof of the Schur product theorem: The Kronecker product $A\otimes M$ of two psd matrices is psd. The entrywise product $A\circ M$ is a principal submatrix of $A\otimes M$: $$A\circ M = ((A\otimes M)_{(i+n(i-1))(i+n(i-1))} : i = 1,\ldots,n).$$All principal submatrices of a psd matrix are psd, so $A\circ M$ is psd.

New blog post with four proofs of the Schur product theorem. Do you know a fifth? www.ethanepperly.com/index.php/20...

New blog post up! In it, I look at the question: how accurate is sketch-and-solve method for least squares? A standard bound suggests the residual is within a 1 + O(η) factor of optimal for an embedding of distortion η. But this isn't the correct answer! www.ethanepperly.com/index.php/20...

Oooo can you share?

Delightful little tale by Nick Trefethen: people.maths.ox.ac.uk/trefethen/ba...

What is your favorite proof of the Cauchy–Schwartz inequality? I wrote about my favorite proof, which uses matrix theory, in a new blog post. Check it out! Also included: a matrix theoretic proof of Jensen’s inequality for 1/x www.ethanepperly.com/index.php/20...

Sorry! This is definitely one of the most "advanced" posts I've written on my blog so far. The earlier posts in my "low-rank approximation toolbox" series might be some help, at least! www.ethanepperly.com/index.php/ca...

Did you know that randomized Nyström approximation of A is equivalent to running the randomized SVD on A⁰ᐧ⁵? This and other surprising facts on this week's blog post on the "Gram correspondence" www.ethanepperly.com/index.php/20...

This whole “advent of research” series of posts by David is really excellent, but I love this one in particular

New blog post up! The randomized Kaczmarz algorithm doesn’t converge for inconsistent systems of linear equations, but—as an estimator for the least-squares solution—it does have an exponentially decreasing bias www.ethanepperly.com/index.php/20...

Randomized Kaczmarz with tail averaging The randomized Kaczmarz (RK) method is a well-known approach for solving linear least-squares problems with a large number of rows. RK accesses and processes just one row at a time, leading to exponen...

Check out the paper! arxiv.org/abs/2411.19877

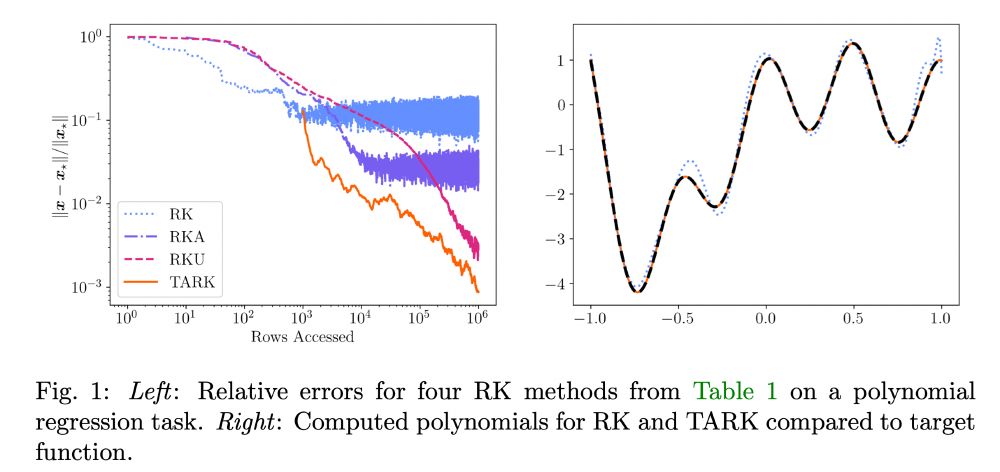
Error for different randomized Kaczmarz methods applied to a least-squares problem. Tail-averaged randomized Kaczmarz (TARK) outcompetes the existing methods

New paper out with Gil Goldshlager and Rob Webber! In it, we show that *tail averaging* can be used to improve the accuracy of the randomized Kaczmarz method for solving least-squares problems. The resulting method, TARK, outcompetes other row-access methods for least squares

Cross-posting this - please join us!

Mailing List link: groups.google.com/g/internatio...
YouTube Channel link: www.youtube.com/@MonteCarloS...

A reminder about NY Theory Day in a week! Fri Dec 6th! Talks by Amir Abboud, Sanjeev Khanna, Rotem Oshman, and Ron Rothblum! At NYU Tandon!

sites.google.com/view/nyctheo...

Registration is free, but please register for building access.

See you all there!

Just created the Starter Pack for Optimization Researchers to help you on your journey into optimization! 🚀

Did I miss anyone? Tag them or let me know what to add!

go.bsky.app/VjpyyRw

The first d columns of an a Haar random matrix from the orthogonal group O(n), yes

A uniformly random matrix with orthonormal rows would be another example

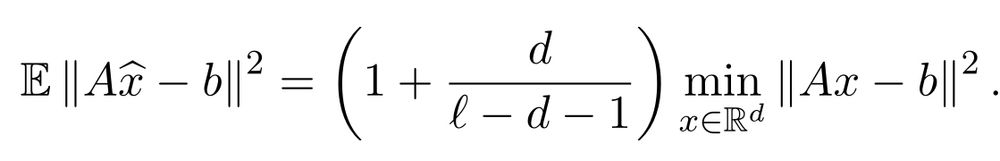
New blog post up presenting some beautiful *exact formulas* for sketched least squares with a Gaussian embedding. These beautiful formulas appear to have only been published as recently as 2020; see post for details! www.ethanepperly.com/index.php/20...

Very excited to be attending #NeurIPS2023 next week where I’ll be presenting my work “Kernel quadrature with randomly pivoted Cholesky” with Elvira Moreno. I’ve written a little blog post to explain what kernel quadrature is and what our approach is to it!