Joseph O'Rourke

Besides #MathSky #MathArt #Geometry #Origami, neglected to include also: #ArtMath #Mathematics and 🧪

Concentric M/V folds.

Each annulus alternates mountain folds with valley folds.
It is not yet proved that this folding "exists" in the sense that only the circular creases are necessary. Strong numerical evidence, but not formally proved.
#MathSky #MathArt #Geometry #Origami

Intertwined annuli.

Curved circular creases of annuli. A construction by Erik and Martin Demaine (all rights reserved). Several annuli intertwined.
#MathSky #MathArt #Geometry #Origami
More examples: erikdemaine.org/curved/)

Cambridge University Press.
www.cambridge.org/core/books/m...
#MathSky #Mathematics 🧪 #Geometry #Origami #MathArt

Cover: The Mathematics of Origami

*The Mathematics of Origami*.
Expected online publication date: December 2025. Print publication: 31 December 2025.
www.science.smith.edu/~jorourke/Ma...
#MathSky #Mathematics 🧪 #Geometry #Origami #MathArt

In fact in this example, 3 guards suffice. Minimal guarding is an NP-hard problem, i.e., intractable.
#Mathematics #MathSky #GraphTheory
www.science.smith.edu/~jorourke/bo...

3-coloring if a triangulated polygon

"Louvre robbery: Could a 50-year-old maths problem have kept the museum safe?" This is a BBC article by Kit Yates about the art gallery theorem. In the figure, four red vertex guards suffice to visually cover the whole polygon. #Mathematics #MathSky #GraphTheory www.bbc.com/future/artic...

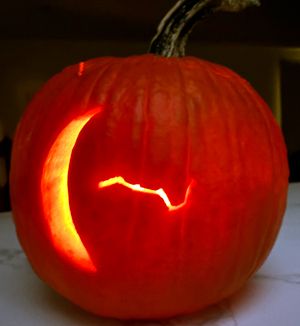
Crescent moon carved into pumpkin.

Crescent Moon. Did you ever notice that the outer convex curve of the crescent is a semicircle, but the inner concave curve is (half of) an ellipse. An ellipse because we are viewing a circle at an angle; a circle projects to an ellipse. #MathSky #Mathematics #Geometry #Pumpkin #Moon

These triangles are known to have a periodic billiard path: (1) All acute triangles. (2) All right triangles. (3) All rational triangles. (4) All obtuse triangles with obtuse angle smaller than 5 pi/8 (the 112.4 deg that I quoted). #MathSky #Mathematics #Geometry #Billiards

Sharp eyes to notice the two perpendicular bounces. Probably not for all triangles, I agree.

Beautiful indeed. And with recent results from the study of translation surfaces.

Triangle w complex periodic orbit.

It is *still* unknown whether or not every triangle admits a periodic billiard trajectory. Every triangle with rational angles does. And so does every obtuse triangle of at most 112.4 deg. "112.5 appears to be a natural barrier."
gwtokarsky.github.io. #MathSky #Mathematics #Geometry #Billiards

Sure. Have them email me, jorourke@smith.edu.

Vertex v mapped to sphere.

Stoker's Conjecture settled by Cho & Kim positively: Every 3D polyhedron is uniquely determined by its dihedral angles and edge lengths, even if nonconvex or self-intersecting (subject to technical restrictions).
doi.org/10.1007/s004...
#MathSky #Mathematics #Geometry #Polyhedra

See also: "Why can't a nonabelian group be 75% abelian?" mathoverflow.net/q/211159/6094

Tetrahedron in a sphere.

What is the probability that 4 points chosen uniformly at random on surface of a sphere form a tetrahedron whose four faces are each acute? Asked on MathOverflow (mathoverflow.net/q/498296/6094) with evidence that the answer is 1/12. But not yet resolved.
#MathSky #Mathematics #Geometry #Probability

Scalloped square tiling.

A monohedral tiling of the plane by "spandrelized" squares.
Each unit square includes a circular arc of a 1/2-radius circle centered at each vertex.
Adams, Colin. "Spandrelized Tilings." Amer. Math. Monthly 132, no. 3 (2025): 199-217.

doi.org/10.1080/0002...
#MathSky #Mathematics #Geometry #Tiling

I wonder in which dimensions is the cylinder/sphere volume ratio rational?
#Mathematics #MathSky #Geometry

Sphere/Cylinder

Archimedes: "Every cylinder whose base is the greatest circle in a sphere and whose height is equal to the diameter of the sphere has a volume equal to 3/2 the volume of the sphere." Cicero found Archimedes' tomb ~137 yrs later with his famous theorem represented.

#Mathematics #MathSky #Geometry

Fig. 22(b)

New tiling results on the arXiv, one of which says that determining whether or not two connected polycubes can together tile R^3 is undecidable (Cor. 5.5). A polycube is an object built by gluing cubes face-to-face. (Unrelated fig.)
arxiv.org/abs/2509.07906
#MathSky #Mathematics #Geometry #Tiling

p.4 of their paper details the construction. "the Noperthedron has 3·30=90 vertices." They set three pts C1,C2,C3 and then apply the cyclic group C_30 to each.

Hexagonal Waterbomb stent.

Believe it or not, origami stents have been explored: Kuribayashi et al., "Self-deployable origami stent grafts ..."
(doi.org/10.1016/j.ms...)
Here I show a hexagonal design built with origami waterbomb crease patterns.
cs.smith.edu/~jorourke/Ma...
#Mathematics #Geometry #MathSky

The Rupert property requires the convex polyhedron P to tunnel by translation through an isometric copy of P. I wonder if twisting while translating would permit any P---even the "Noperthedron"---to pass through itself? #Mathematics #Geometry #MathSky

Yes, the authors clearly had fun! :-)

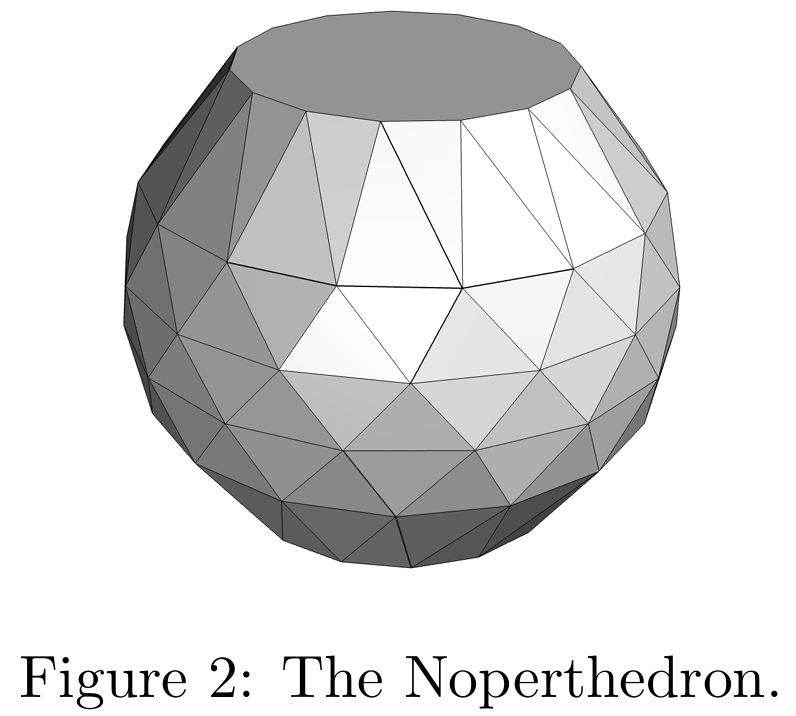
Non-Rupert convex polyhedron.

The conjecture that every convex polyhedron is Rupert is settled in the negative! The convex body in the image cannot pass straight through a hole inside itself.
arxiv.org/abs/2508.18475
#Mathematics #Geometry #MathSky

*Visual Complex Analysis* by Tristan Needham. global.oup.com/academic/pro...

A surprising result: 3-space can be filled with disjoint geometric unit-radius circles. So each point of R^3 lies on exactly one circle. The circles may even be chosen to be unlinked. M. Jonsson and J. Wästlund: www.jstor.org/stable/24493....
#MathSky #Geometry #Mathematics

Optimal 8-vertex isoperimetric polyhedron? I know from Marcel Berger's Geometry Revealed: A Jacob's Ladder to Modern Higher Geometry (p.531) that it is not yet established which polyhedron in $\mathbb{R}^3$ on 8 vertices achieves the optimal

Henry Cohn figured that out: Again, not the cube:
mathoverflow.net/a/73941/6094

Max volume 8-vertex inscribed polyhedron.

You might guess that the maximal volume 8-vertex polyhedron inscribed in a unit sphere is the cube. But it's not even close : cube 1.54; 8-vertex max 1.82. Proved by Berman and Hanes in 1970. V=8, E=16, F=10. #MathSky #Geometry #Mathematics

Net for 40-vertex top & bottom prismoid.

Angel-wing net (edge-unfolding) of a nearly flat prismoid, top & bottom two 40-vertex regular polygons. No mathematical significance, just an attractive image. (The two red edges are not cut.) #MathSky #Geometry #Mathematics #MathArt