
rules for Where's Waldo
06.10.2025 13:25 — 👍 0 🔁 0 💬 1 📌 0@conitzer.bsky.social
AI professor. Director, Foundations of Cooperative AI Lab at Carnegie Mellon. Head of Technical AI Engagement, Institute for Ethics in AI (Oxford). Author, "Moral AI - And How We Get There." https://www.cs.cmu.edu/~conitzer/

rules for Where's Waldo
06.10.2025 13:25 — 👍 0 🔁 0 💬 1 📌 0
Apparently aging really does happen in years.
05.10.2025 12:33 — 👍 1 🔁 0 💬 1 📌 0
time and clocks
04.10.2025 02:50 — 👍 5 🔁 0 💬 0 📌 0
"is it possible for any animal to fly from brooklyn to manhattan"
02.10.2025 23:25 — 👍 5 🔁 0 💬 0 📌 0
trash day
01.10.2025 02:43 — 👍 1 🔁 0 💬 0 📌 0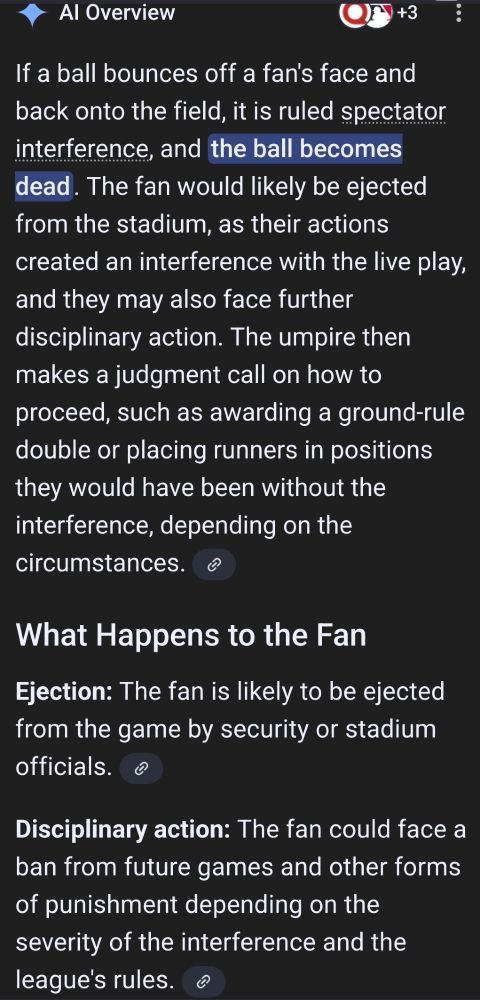
adding insult to injury
30.09.2025 02:20 — 👍 0 🔁 0 💬 0 📌 0
Please hold still while the AI gets the information into your brain most efficiently.
28.09.2025 02:55 — 👍 4 🔁 0 💬 1 📌 0
Excited our paper "AI Testing Should Account for Sophisticated Strategic Behaviour" was accepted to the first NeurIPS position paper track! We argue AI systems may act strategically w.r.t. the possibility they are currently being tested & game theory helps address this.
arxiv.org/abs/2508.14927

planes
26.09.2025 02:09 — 👍 1 🔁 0 💬 0 📌 0
more geography
25.09.2025 02:22 — 👍 2 🔁 0 💬 0 📌 0
borders
23.09.2025 19:02 — 👍 73 🔁 13 💬 5 📌 4
I got to give the opening lecture for the 2025 Cooperative AI Summer School and the video is now online! "Foundations and Frontiers of Cooperative AI" www.youtube.com/watch?v=nfnb... @coop-ai.bsky.social
22.09.2025 20:18 — 👍 4 🔁 0 💬 0 📌 0
BTW the continuation of this (citing Healthline!):
22.09.2025 15:15 — 👍 1 🔁 0 💬 0 📌 0
Don't you hate it when you have your eyes closed just when you take a picture?
21.09.2025 17:29 — 👍 3 🔁 2 💬 1 📌 0
"which country is two countries to the north of mexico"
20.09.2025 20:38 — 👍 1 🔁 1 💬 0 📌 0
Congratulations to Emin Berker for receiving the Best Talk Award at COMSOC'25! (in the picture with coauthor Edith Elkind; paper arxiv.org/abs/2502.16973 )
19.09.2025 19:27 — 👍 7 🔁 0 💬 1 📌 0What would you think if you ran into a couple with a baby who told you they have two other kids?
18.09.2025 01:14 — 👍 0 🔁 0 💬 1 📌 0
"if a baby has two siblings what is the probability it is the oldest?"
17.09.2025 19:16 — 👍 0 🔁 0 💬 1 📌 0
tennis
16.09.2025 21:28 — 👍 1 🔁 0 💬 0 📌 0
"how many unbreakable 1 by 1 by 1 blocks fit in a 2.9 by 2.9 by 2.9 box?"
16.09.2025 00:31 — 👍 4 🔁 0 💬 0 📌 0
occupancy limits
14.09.2025 13:19 — 👍 4 🔁 1 💬 0 📌 0
lion puzzle, part 2 -- I'll mark this solution as correct but with some drawbacks
13.09.2025 17:06 — 👍 1 🔁 0 💬 0 📌 0

lion puzzle, part 1
12.09.2025 20:25 — 👍 2 🔁 0 💬 0 📌 0
"what if i put the stamp inside the envelope?"
12.09.2025 01:43 — 👍 2 🔁 0 💬 0 📌 1

"what if i stand behind someone who stands in front of me"
10.09.2025 23:18 — 👍 1 🔁 0 💬 0 📌 0
depths of sunken ships, part 2 (let's see who can explain this one)
09.09.2025 19:02 — 👍 0 🔁 0 💬 0 📌 0
depths of sunken ships, part 1
08.09.2025 16:56 — 👍 1 🔁 0 💬 0 📌 0
Good luck to Sinner and Alcaraz in the US Open final today! ... even though their trajectory in the tournament so far is not even logically possible.
07.09.2025 12:53 — 👍 2 🔁 0 💬 1 📌 0Did it get the colors of the apples right?
06.09.2025 22:33 — 👍 1 🔁 0 💬 1 📌 0
color photography
06.09.2025 19:30 — 👍 1 🔁 0 💬 2 📌 0