Shreyas Srinivas

To all the people mocking LLMs because it's "just matrix multiplication (linear algebra):"

Careful there! You're going to piss off the quantum physicists

YouTube video by Computerphile Gödel's Incompleteness Theorem - Computerphile

Thorsten Altenkirch explains Gödel's Incompleteness Theorem on @computerphile.bsky.social, and shows some definitions in #LeanLang! 🎯

Watch here: www.youtube.com/watch?v=IuX8...

Understanding Quantum Information and Computation This is a course on the theory of quantum computing. It consists of 16 lessons, each with a video and written component, covering the basics of quantum information, quantum algorithms (including query...

After 3 1/2 years of work my course on quantum computing is finally finished — the "Director's Cut" of Understanding Quantum Information and Computation is now available.

arxiv.org/abs/2507.11536

Table of contents of the monograph

Reminder/plug: my graduate-level monograph on "Topics and Techniques in Distribution Testing" (FnT Comm. and Inf Theory, 2022).

📖 ccanonne.github.io/survey-topic... [Latest draft+exercise solns, free]
📗 nowpublishers.com/article/Deta... [Official pub]
📝 github.com/ccanonne/sur... [LaTeX source]

YouTube video by Thatchaphol Saranurak Lecture 4.1: Amortized Analysis: Bank account method, Binomial heaps, Hollow heaps

This lecture provides a gentle introduction to amortized analysis.

For experts: At the end, I explained Hollow Heaps, an optimal heap like Fibonacci heaps, but simpler! Surprisingly, I have not seen video lectures on this before.

www.youtube.com/watch?v=8mHa...

I must note that it would be harder to check the correctness of definitions and theorems in such an autoformalisation than review the pen and paper version in a conference.

This is not to say that they can’t get better at this stuff, but the bigger the formalisation effort, the less one should trust an AI with the definitions and theorem statements. And even after ensuring correctness, such a formalisation would be devoid of all the uses one could put it to.

In general there is a wide gap between what ML researchers achieve in experiments and how well it works in practice. In addition, there is a deployment gap. In our equational theories project we explicitly noted that modern AI was extremely underwhelming.

Yes. This was discussed in the lean Zulip. I don’t take it too seriously for the following reason. This tool was provided a very fine grained blueprint. I can imagine that for the typical SODA paper, even with all the prerequisite material existing in some library, it would be a 1000 pages.

I am inclined to believe that AI tools will have the same effect on formal proofs. They might take users to intractable proof states and give up when used or modify definitions incorrectly to get proofs accepted.

Markus Himmel has written a blog post about how to write a simple imperative program in Lean and then how to verify that the program is bug-free.

markushimmel.de/blog/my-firs...

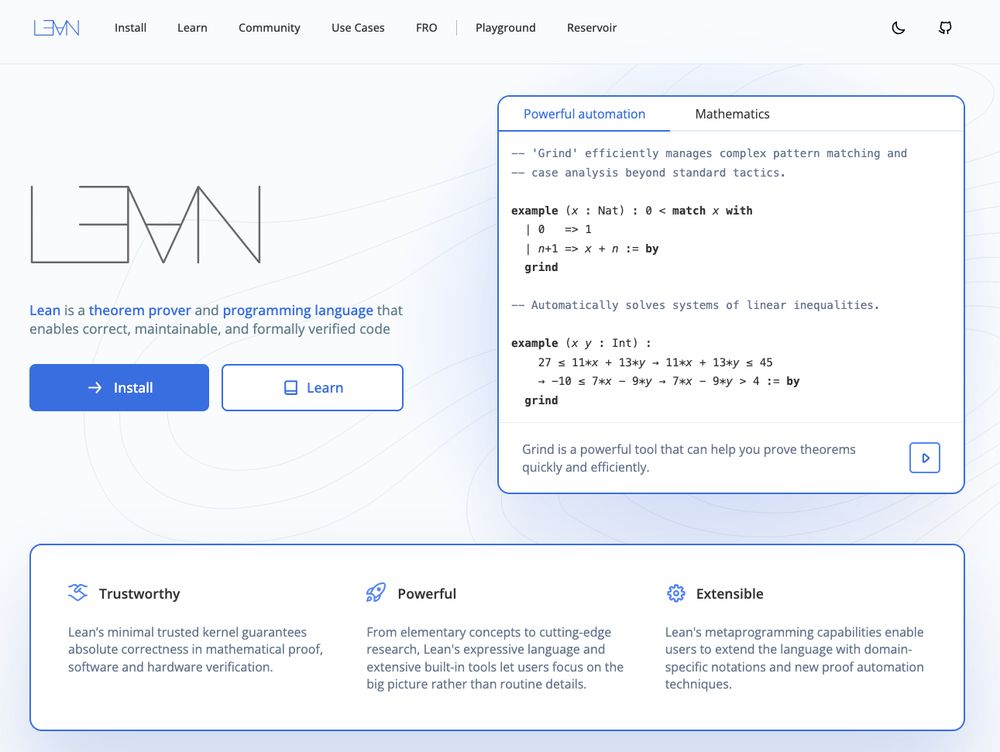
📣 We're excited to share the new lean-lang.org!

Relaunching our website was a key deliverable in our Year 2 roadmap to provide "improved navigation and access to valuable content, resources, and tools." We hope you like it!

#LeanLang #LeanProver

YouTube video by Macclesfield Museums Binary and the Jacquard Mechanism - demonstration

I finally understand the mechanism of the Jacquard loom. Still cannot fathom how designers program the holes.

youtu.be/pzYucg3Tmho

How Does Graph Theory Shape Our World? | Quanta Magazine Maria Chudnovsky reflects on her journey in graph theory, her groundbreaking solution to the long-standing perfect graph problem, and the unexpected ways this abstract field intersects with everyday…

Graph theorist Maria Chudnovsky proved the strong perfect graph theorem, which was proposed back in the 1960s. Tune in to “The Joy of Why” with co-host @jannalevinastro.bsky.social:

Our ICALP 2025 paper is now available here! We present the first example of a locally checkable labeling problem that becomes much easier to solve with distributed algorithms if you have access to shared randomness.
doi.org/10.4230/LIPI...

*most of the reasons that I am referring to stem from academic publishing culture operating across a number of subfields of CS

We didn’t do it till now for reasons that have nothing to do with AI. It is a confluence of a number of factors, too long to list here. We are able to consider a formal algorithms library at this point because a lot of metaphorical stars are aligned right now.

And the community needs to recognise that this is actually research into its own concepts and methodologies. A reappraisal in the same sense that Cauchy and co put calculus on firm foundations. That’s basically non existent right now.

I am not optimistic about implementations. A lot of theory is simply not implementable in a practical sense. Even to empirically establish asymptotics we would need humongous input instances. However this might result in a reappraisal of the value of chasing asymptotics to no end (Goodhart’s law).

This is in some sense an intermediate abstract specification that an implementation of an algorithm “refines”. We commonly call this pseudocode.

But all this requires a unified library a la mathlib. Not one thousand different and fragmented formalisations (which is the case in PL). It requires searching for common patterns and expressing them with good definitions.

Closely related to this, our literature is a complete mess at this point. I see so many models of computing which need to have their definitions nailed down. Further, there is literature search. When formalizing in lean, I often search for existing theorems automatically.

That being said I am not wholly on board the notion that AI will ever usefully autoformalize papers. For the algorithms community, the real utility in formalisation is to actually understand and extract useful abstractions and reuse theorems and “algorithmic technicques” more effectively.

The first thing we need to accept is that our field is not about implementable algorithms. Trying to formalise implementations is quite simply infeasible. Instead we need to recognise that we write what someone on the lean server helpfully called combinatorial procedures.

I am actually working on solving this problem to be upfront.

I don’t think lean rules out anything in TCS

This problem of brittleness in over powerful automation and difficulty of debugging them is already familiar to users of SAT and SMT solvers. If we create a suitable modular structure for our proofs, then we can expect to contain this brittleness. But this still requires formalisation to work.

The ideal use case is where someone has laid out a blueprint for the proofs down to the lemma hierarchy. Then automation can be used to fill in proofs of lemmas in seconds where a human user could still spend a few hours to write out the proof formally if the automation fails.

There are serious drawbacks to relying on overpowerful Blackbox automation. What we really need is composable automation whose effects are bounded and limited so that we can debug when something goes wrong.

I can’t predict these numbers currently. Two examples : In Terry Tao’s video from our ETP, the AI often dropped him into super difficult spots. In Alex Kontorovich’s formalisation of a conjecture statement, the AI had him convinced that he got it right leaving behind subtle but critical bugs.