David Beers

New interdisciplinary math+bio paper! Mouse liver assembloids model periportal architecture and biliary fibrosis. In vitro assembloids modelling the mouse liver periportal region were built to study processes causing scarring (cholestatic injury/biliary fibrosis) and the shape change this causes.

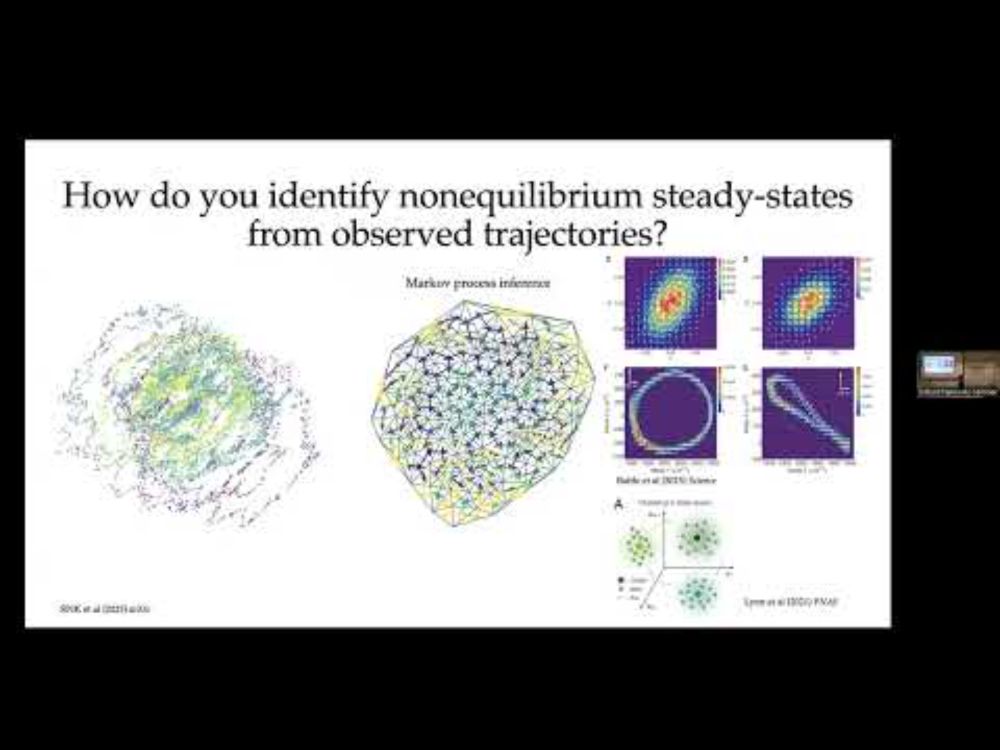
Speaking at NetSci2025 about our recent Learning on Graphs paper.

We build up a theoretical and applied approach to use Hodge theory on graphs to study stochastic systems!

arxiv.org/pdf/2409.07479

#NetSci2025

Whether the converse of the above tweet is true, we know not. Finally, were able to tell a similar story about local identifiability of Čech persistence, except it involves hypergraphs instead of graphs, and a rigidity theory that is, to our knowledge, new.

10/10

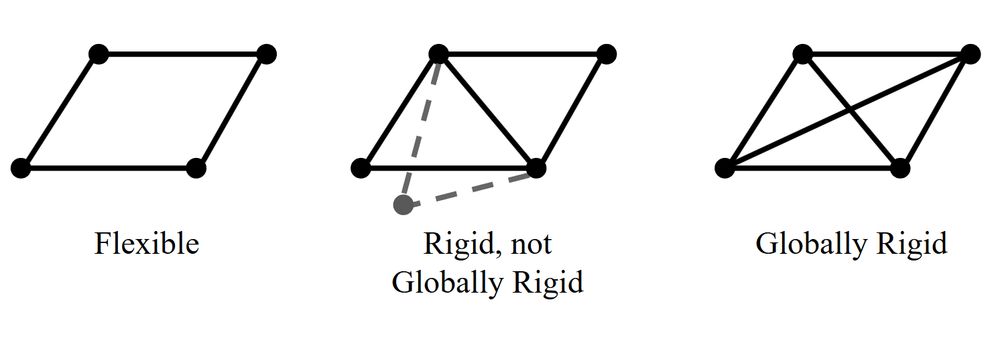
Using a modern rigidity theory result of Gortler, Theran, and Thurston, we also proved that if G is globally rigid, then P is identifiable. G being globally rigid means you cannot teleport points in P without preserving edge lengths in G, unless you teleport via isometry.

9/10

As it turns out, it is difficult to figure out when a graph is rigid in general- indeed rigidity theory is an active subject in real algebraic geometry. This suggests that it is hard to figure out which point clouds are locally identifiable.

8/10

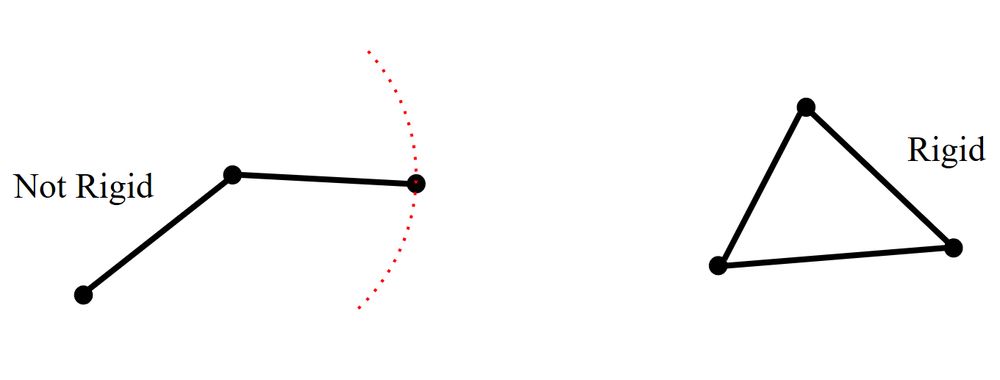
G being rigid means we can't wiggle the points in P without changing the edge lengths of G, unless we wiggle the points in P via isometry.

7/10

Here is how to find out if P is locally identifiable (under Vietoris-Rips PH). Make a graph G with vertex set P and any edge whose inclusion in the V-R filtration coincides with a change in topology. Any generic P is locally identifiable exactly when G is rigid.

6/10

Its natural to ask which point clouds are best described by PH. These are the point clouds P such that if Q has the same PH, then P and Q are isometric. Such a P is called identifiable. If P is isometric to any NEARBY Q with the same PH then P is called LOCALLY identifiable

5/10

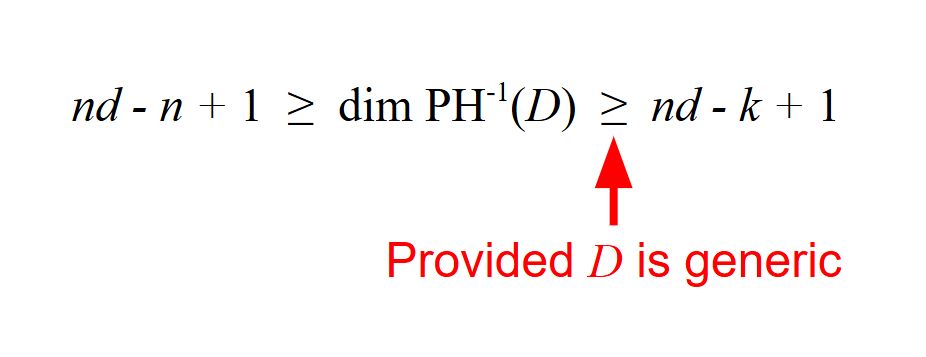
We can quantify how big a level set is by computing its dimension. If D is a family of barcodes (one for each homological degree) with k distinct endpoint values, we showed the following inequalities hold (see picture)

4/10

What we are interested in this paper is how descriptive this mapping is. One way to ask this is to ask how big the level sets are. Big level sets mean many point clouds have the same barcodes, so PH is not very descriptive at barcodes with big level sets.

3/10

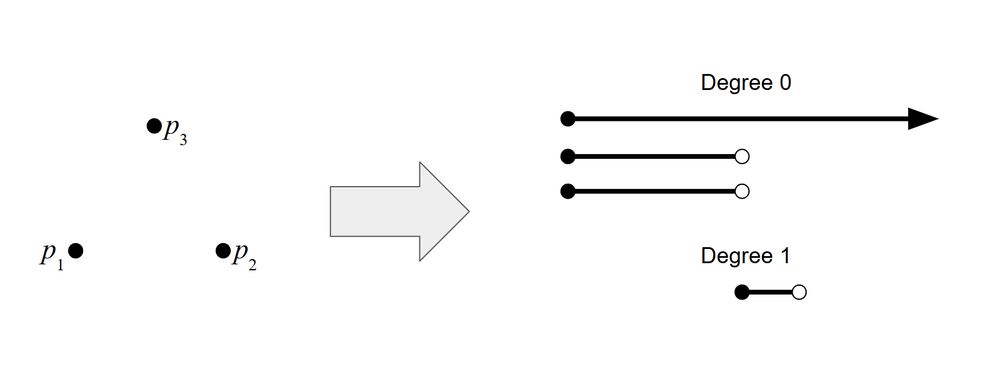
As many of my faithful followers will be aware, using either Čech or Vietoris-Rips persistent homology (PH) we get a barcode in each homological degree from any point cloud. So we have a mapping PH:
Point clouds with n points in d dimensions
->
Barcodes

2/10

I posted about this paper this a while ago on another website, but figured I'd post it here now that I have a few followers. (Joint with @haharrington.bsky.social, Jacob Leygonie, @uzulim.bsky.social, and Louis Theran).

arxiv.org/abs/2411.08201

1/10

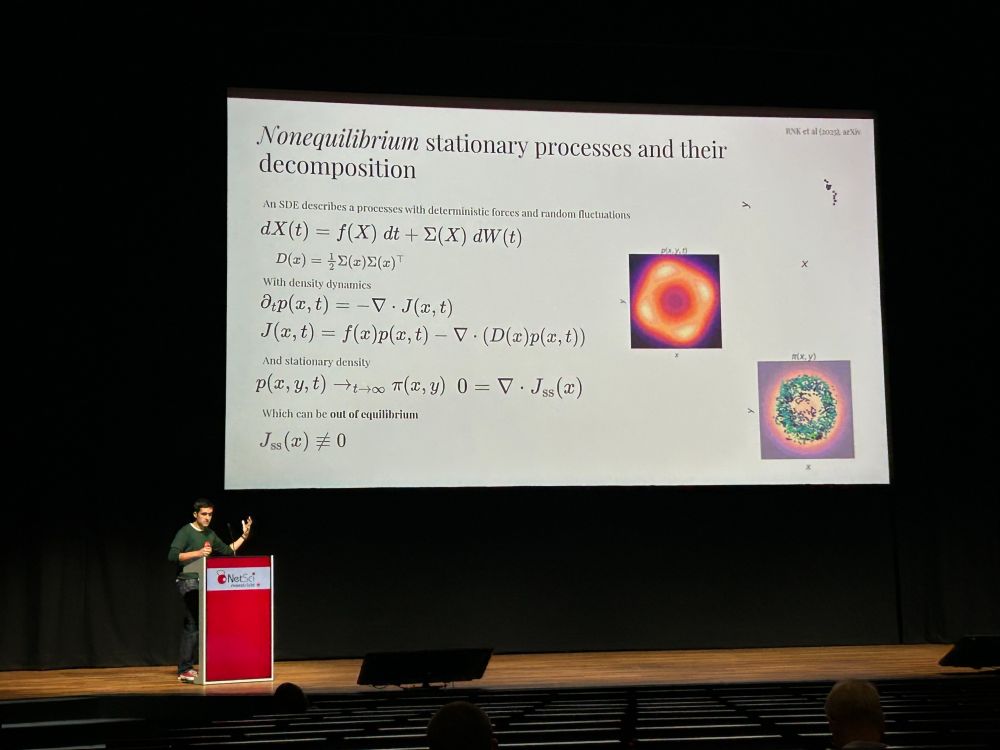
YouTube video by Fresh from the ArXiv Ramon Nartallo-Kaluarachchi: Non-equilibrium steady-states, from diffusion to digraphs

Last week, I gave the Networks seminar here at Oxford on:

'Nonequilibrium steady-states: from diffusion to digraphs',

talking about some of my recent work on discrete approximations of nonequilibrium diffusions. It is available online:
www.youtube.com/watch?v=ezep...

:)