Daniel Musekamp

Active Learning for Neural PDE Solvers Solving partial differential equations (PDEs) is a fundamental problem in engineering and science. While neural PDE solvers can be more efficient than established numerical solvers, they often require...

Coauthors: Marimuthu Kalimuthu, David Holzmüller (@dholzmueller.bsky.social), Makoto Takamoto, and Mathias Niepert (@mniepert.bsky.social)
Paper: arxiv.org/abs/2408.01536
Code: github.com/dmusekamp/al...
9/

Limitations:
- Future work is needed to look at the missing advantage of AL on CNS.
- Benchmark does not include irregular grids or complex geometries, which might be
an interesting setting for AL due to the more complex input space. 8/

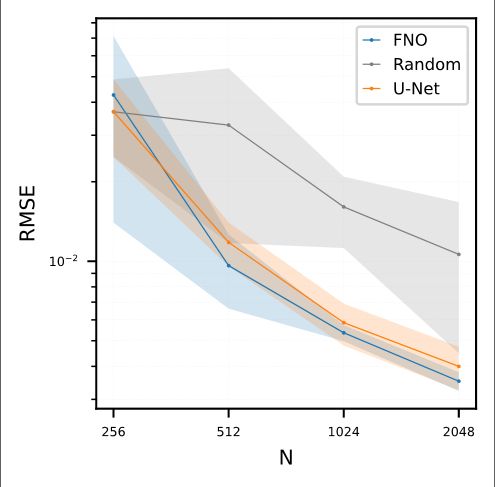
The generated data is also beneficial for surrogate models which have not been used to select the data. Here, we compare the accuracy of a U-Net with data selected randomly or using an FNO or the U-Net itself as the base model. 7/

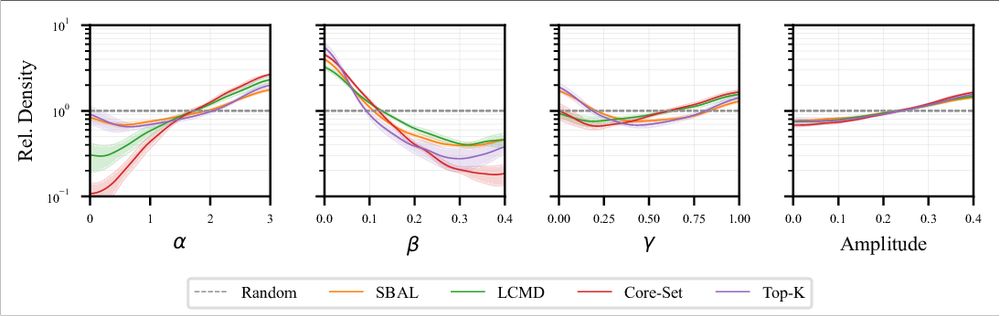
A look at the distribution of the selected parameters shows that the standard deviation between random repetitions is small, indicating that the AL procedure reliably produces very similar datasets. 6/

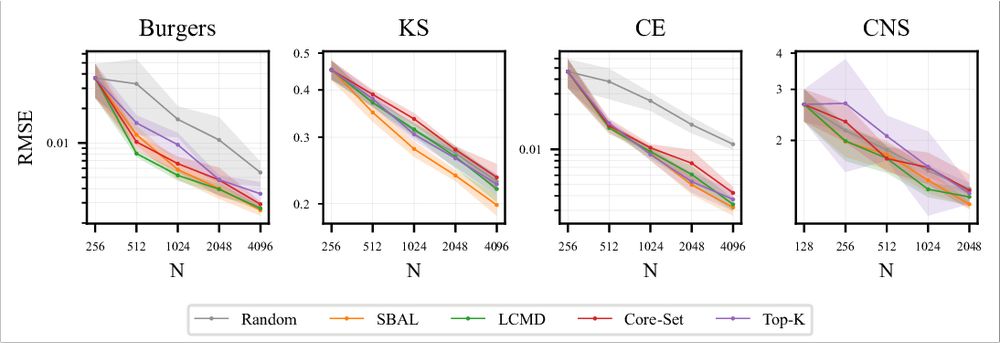
The experiments show that AL reduces the average errors by up to 71% compared to random sampling for the same amount of selected data. Especially, Stochastic Batch Active Learning and LCMD perform well. 5/

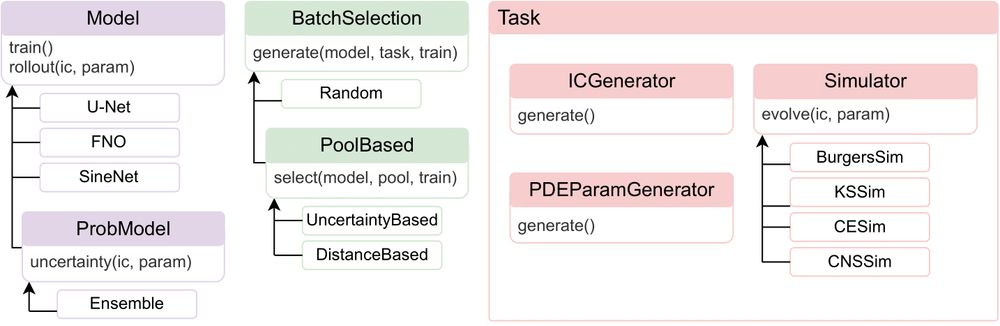
To facilitate the research of AL on autoregressive neural PDE solvers, we introduce AL4PDE, an extensible, modular benchmark framework. It provides:
- Parametric PDEs such as incompressible Navier-Stokes
- Surrogate models (U-Net, FNO, SineNet).
- AL algorithms such as SBAL, CoreSet, or LCMD. 4/

AL presents a promising solution by only selecting the most informative training samples, reducing the number of simulations required to train neural PDE solvers. As high-dimensional, spatio-temporal time series, PDEs are a challenging domain for AL algorithms. 3/

Solving partial differential equations (PDEs) is fundamental in science & engineering. Neural PDE solvers can offer advantages such as speed and differentiability but require large datasets from costly numerical simulations. 2/

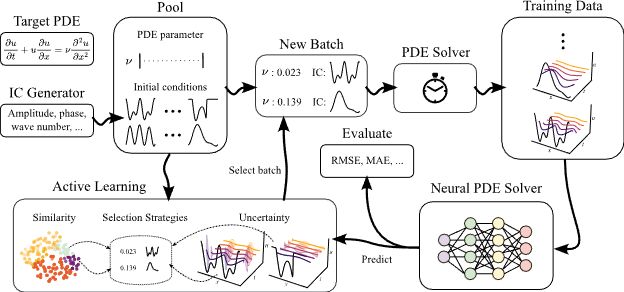
Neural surrogates can accelerate PDE solving but need expensive ground-truth training data. Can we reduce the training data size with active learning (AL)? In our NeurIPS D3S3 poster, we introduce AL4PDE, an extensible AL benchmark for autoregressive neural PDE solvers. 🧵

AL presents a promising solution by only selecting the most informative training samples, reducing the number of simulations required to train neural PDE solvers. As high-dimensional, spatio-temporal time series, PDEs are a challenging domain for AL algorithms. 3/

Solving partial differential equations (PDEs) is fundamental in science & engineering. Neural PDE solvers can offer advantages such as speed and differentiability but require large datasets from costly numerical simulations. 2/