Nathanael Bosch

GitHub - pnkraemer/probdiffeq: Probabilistic solvers for differential equations in JAX. Adaptive ODE solvers with calibration, state-space model factorisations, and custom information operators. Compa... Probabilistic solvers for differential equations in JAX. Adaptive ODE solvers with calibration, state-space model factorisations, and custom information operators. Compatible with the broader JAX s...

Thanks! Yes they should also work for larger nonlinear systems as long as they are not too stiff. And there is also a Python implementation by @pnkraemer.bsky.social: github.com/pnkraemer/pr...

GitHub - nathanaelbosch/ProbNumDiffEq.jl: Probabilistic Numerical Differential Equation solvers via Bayesian filtering and smoothing Probabilistic Numerical Differential Equation solvers via Bayesian filtering and smoothing - nathanaelbosch/ProbNumDiffEq.jl

And because methods are only useful if people can actually use them: I wrote ProbNumDiffEq.jl to make all of this accessible. Give it a try!

💻 github.com/nathanaelbos...
📖 nathanaelbosch.github.io/ProbNumDiffE...
▶️ www.youtube.com/watch?v=iH_G...

6/6

There are many more things that I'd love to write about - e.g. robust parameter inference in neuroscience ODEs - but I think my thesis does a better job at explaining everything.

📄 Full thesis: tobias-lib.uni-tuebingen.de/xmlui/handle...

5/6

Two more examples: We can add linear ODEs to the prior to create a probabilistic version of "exponential integrators". onlinear information (e.g. conservation laws) can be included in the likelihood to get more plausible solutions - see gif.

[2] tinyurl.com/2av3e4te
[3] tinyurl.com/bddfkwcu

4/6

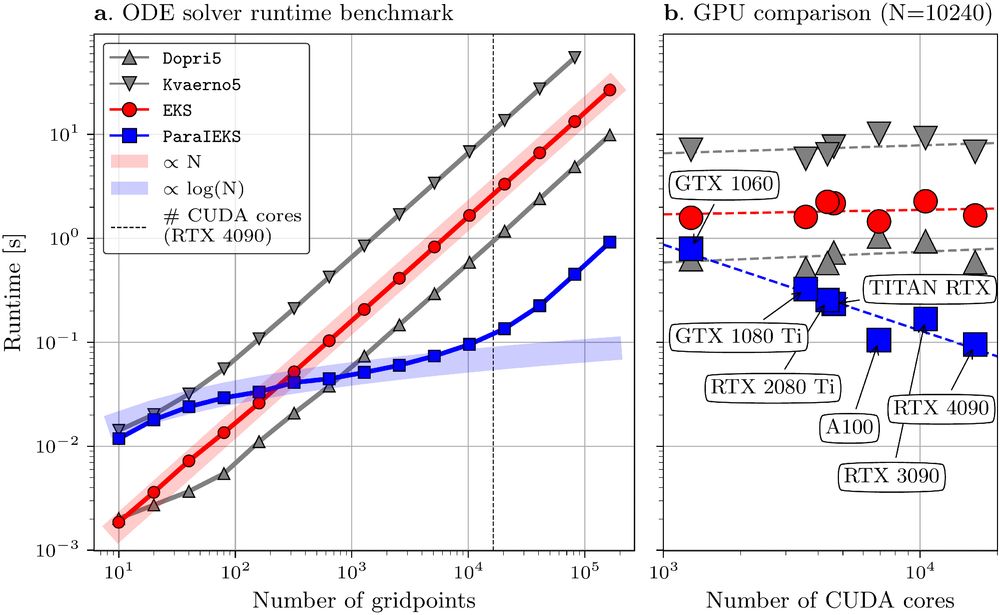
It turns out that this framework is quite convenient: You can easily customize each building block - prior, likelihood, inference - to adjust the solver and its properties. For example, by using a time-parallel smoother we obtain a parallel-in-time ODE solver!

[1] www.jmlr.org/papers/v25/2...

3/6

The main trick is to reformulate "solving an ODE" as "Bayesian state estimation" by turning the ODE into a nonlinear observation model. With a suitable prior - a Gauss-Markov process - you can solve the resulting problem with Bayesian filtering to obtain a probabilistic numerical ODE solution.

2/6

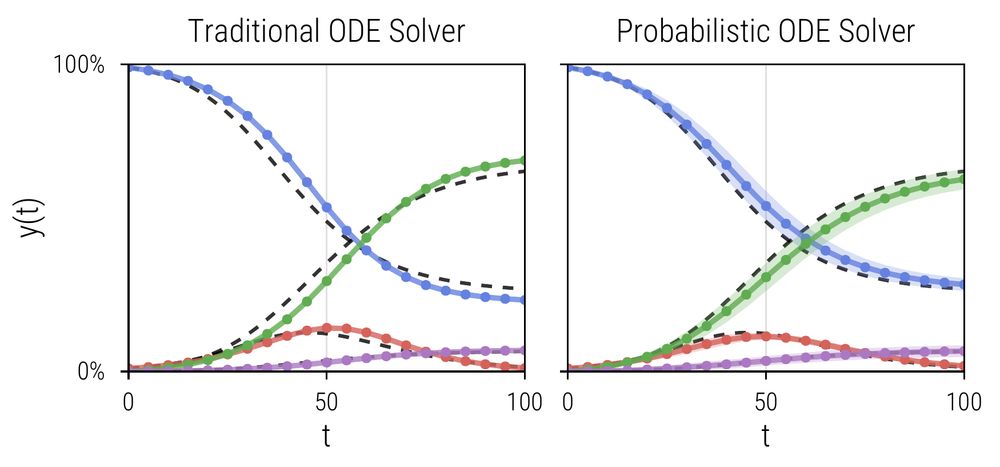
🎉 My PhD dissertation is now online! Traditional ODE solvers compute a single solution estimate - Probabilistic solvers also tell you how reliable they are! In my PhD, I established them as a Flexible and Efficient Framework for Probabilistic Simulation and Inference.
📄 tinyurl.com/mt3sffb

🧵 1/6

🙋

We are organising the First International Conference on Probabilistic Numerics (ProbNum 2025) at EURECOM in southern France in Sep 2025. Topics: AI, ML, Stat, Sim, and Numerics. Reposts very much appreciated!

probnum25.github.io