Max Brodeur

Euclid’s Elements is the second-most printed and studied book in history — after the Bible.

Written around 300 BC in ancient Greece, this edition is its first English translation (1570). It remained a core math textbook well into the 20th century.

04.08.2025 10:25 — 👍 0    🔁 0    💬 0    📌 0

Euclid, Newton & Turing

This weekend, at the John Rylands Library in Manchester, I finally found a historical copy of Euclid’s Elements.

And right next to it: Newton’s Principia and Turing’s handwritten notes. Completely overwhelming.

04.08.2025 10:25 — 👍 0    🔁 0    💬 1    📌 0

Smooth-Rolling Knots Our optimized knots (bottom) roll smoothly, i.e., their centre of mass is always at the same distance from the rolling plane. We generate smooth rolling torus knots with increasing topological complex...

Our paper, videos, and 3D models are available here:
go.epfl.ch/smooth_rolling_knots

31.07.2025 17:27 — 👍 2    🔁 0    💬 0    📌 0

And they work in real life too :)

Smooth-rolling objects require virtually no force to start moving – even with low friction, they roll.

31.07.2025 17:27 — 👍 4    🔁 0    💬 1    📌 0

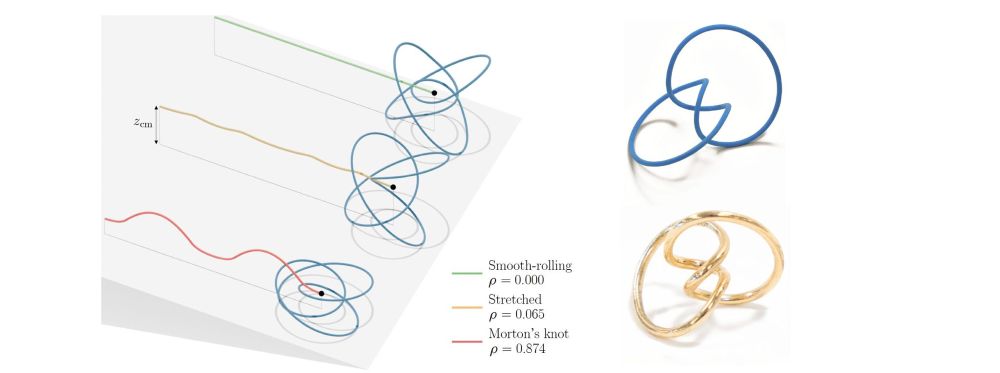
An object is “smooth-rolling” if its center of mass remains at a constant height while it rolls.

We created knots with this property by combining Morton’s knots with Two-Disk Rollers.

31.07.2025 17:27 — 👍 4    🔁 0    💬 2    📌 0

Smooth-rolling knots!

At @markpauly.bsky.social’s lab, we found a way to optimize knots for smooth rolling.

I presented our work at Bridges 2025 – the conference for #MathArt.

More below ↓

31.07.2025 17:27 — 👍 31    🔁 4    💬 2    📌 1

Thank you Keenan — really means a lot!

Your Repulsive Curves are actually what got me working on knots in the first place. :)

29.07.2025 20:47 — 👍 3    🔁 0    💬 1    📌 0

Each number becomes a binary vector representing its prime divisors:

1 → [0, 0, 0, …]
2 → [1, 0, 0, …]
3 → [0, 1, 0, …]
6 (2×3) → [1, 1, 0, …]
30 (2×3×5) → [1, 1, 1, 0, …]

Each bit = “is divisible by the n-th prime?”

29.07.2025 20:01 — 👍 0    🔁 0    💬 0    📌 0

Here are the first 8 million integers, rendered by John Healy.

johnhw.github.io/umap_primes/...

29.07.2025 20:01 — 👍 1    🔁 0    💬 1    📌 0

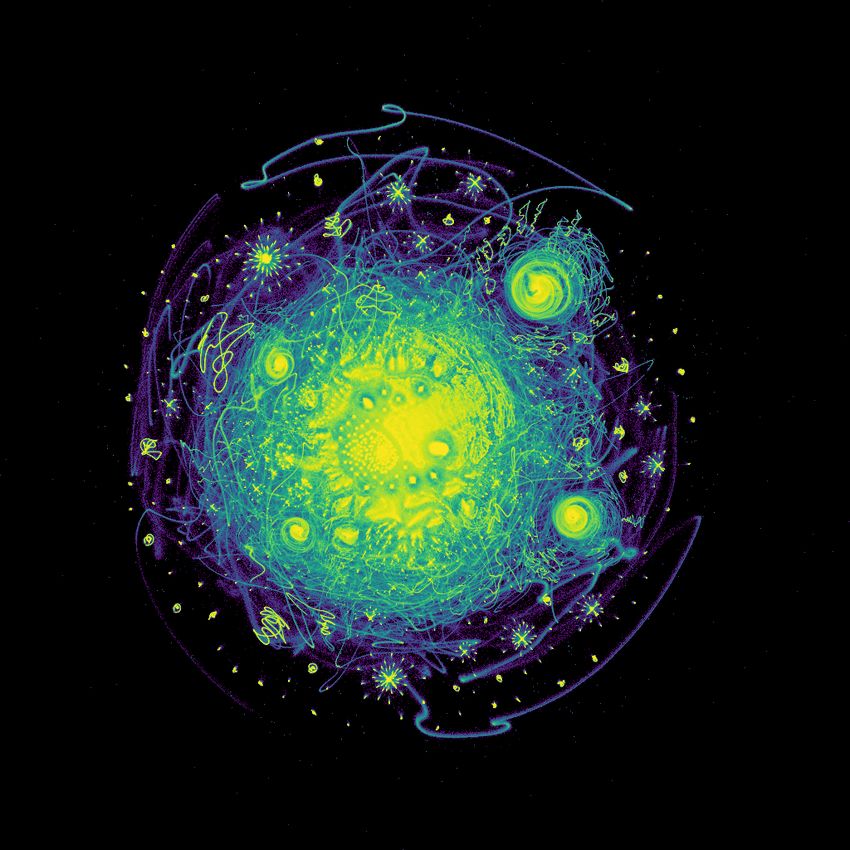
What is the hidden structure of the natural numbers?

In the UMAP paper, @lelandmcinnes.bsky.social et al. embedded the integers as binary vectors of their prime factors.

This UMAP visualization of 30 million integers reveals a fractal-like geometry.

#UMAP #mathart #dataviz #numbertheory

29.07.2025 20:01 — 👍 6    🔁 0    💬 2    📌 0