Original Math Designs

Congratulations!

Orange goo containing plankton floats over and into the fractal surface of infinite holes. The surface is based upon an Apollonian gasket.

“Infinite Holes
and the Cosmic Goo”

10 inch square

I was delighted to learn that this #watercolor and pigment ink #painting won Best Photograph, Painting, or Print at the MAA Mathfest Art Exhibit 2025.

#mathart 
Available

Angled cup featuring a hand painted design resembling the Cassini capture of Earth from Saturn as the "pale blue dot"

Angled cup featuring a hand painted design resembling the Cassini capture of Earth from Saturn as the "pale blue dot" (side)

Angled cup featuring a hand painted design resembling the Cassini capture of Earth from Saturn as the "pale blue dot" (top)

Pale Blue Dot 🌎🪐
(Commission)

Ages ago, I supported a kickstarter with a fancy version of a spirograph called "Hypnograph." I had trouble getting it to work when it arrived, but as I'm planning a math-art class, I broke it out and lo and behold, it works!

I'll put a photo of the final image in a reply post.

#mtbos #mathart

The companion image in a dawn-like palette:
www.diffgeom.com/product/roll...
www.diffgeom.com/product/canv...
#MathArt #MathSky

The cover of "An invitation to Real Analysis." The bottom half depicts a fair but not cloudless sky edged in the bottom corners by reaching branches of tall oaks tinged with spring green. A torus wrapped by a blue-and-cyan solenoid curve of slope pi fills the sky.

My new textbook "An Invitation to Real Analysis" is available for pre-order on August 21. A blog post for prospective instructors briefly explains motivations and choices, from definitions to terminology to notation:

www.diffgeom.com/blogs/around...

#MathSky #ITeachMath

Qualitatively yes!

Thinking of actual oranges, all spirals around the poles do this S-shaped thing to some extent. If we wanted a quantitative model, I expect 1. the details are Hard, but 2. something like a spiral of unwinding (constant separation between turns) might be a better fit...? :)

Very late to the party (but did read the comments :)
To me, the third equality is the issue: If sqrt(-1) connotes a single complex number, equalities 4 and 5 are correct for either choice of sign
If instead sqrt is 2-valued, then equalities 1 and 4 are wrong. That's ... awkward

Inspired by @anniekp.bsky.social and @aliensunset.bsky.social, I created this beautiful piece of mathematical art! Hitomezashi stitching!

To read about a bit about how I stumbled on this, read on!

samjshah.com/2025/08/13/h...

#mtbos #mathart

A family of randomly-chosen double spirals in a red-gold palette against a twilight gradient from light gold to deep blue, suggesting cirrus clouds at sunset.

Loxodromes, spirals on a sphere that meet each longitude at the same angle, map under stereographic projection to the double-spirals shown.

www.diffgeom.com/blogs/about-...

www.diffgeom.com/product/roll...
www.diffgeom.com/product/canv...

#MathSky #MathArt #ITeachmath

Randomly-chosen "longitude" and "latitude" circles in a red-gold palette filling the sky against a twilight gradient from light gold to deep blue.

Poles of a sphere map under stereographic projection (from a third point) to two points in a plane. Longitudes map to circles through both points; latitudes map to "orthogonal" circles. Read more:
www.diffgeom.com/blogs/about-...

www.diffgeom.com/product/roll...

#MathSky #MathArt #ITeachmath

A mathematical sculpture made of 60 interwoven swirly pieces of green glass acrylic, held together with white plastic zip ties

Hey neat!

I was one of three awards at the MAA math fest Art exhibition: Honorable Mention for Ice Orb.

#mathart

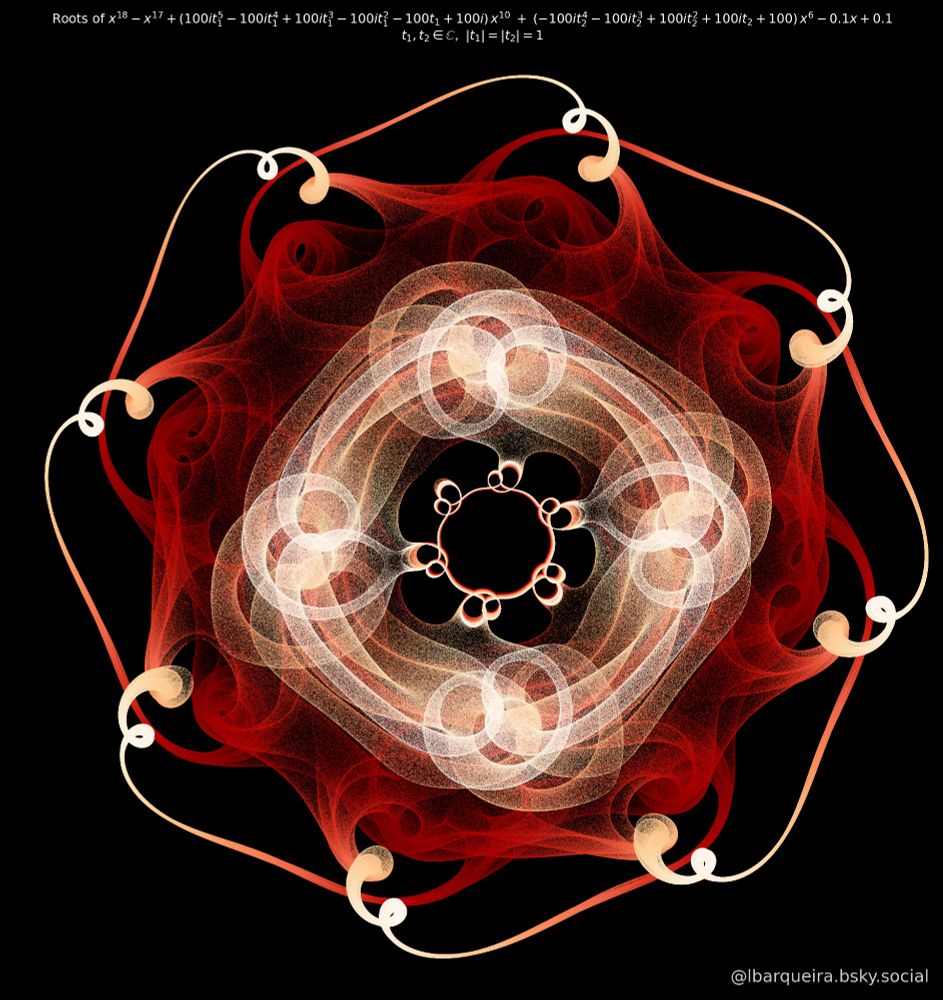
Exploring the roots of an 18th-degree complex polynomial x^18−x^17+(100it1^5−100it1^4+100it1^3−100it1^2−100t1+100i)·x^10+(−100it2^4−100it2^3+100it2^2+100it2+100)·x^6−0.1 x+0.1 where t₁,t₂ are complex numbers on the unit circle. z-axis and color encode Im(t1).

Roots of complex polynomial
Inspired by ‪the work of @sconradi.bsky.social
#MathArt #Python #CodeArt #SciArt #CreativeCoding #Math

Sea Salt

#Maxon #C4D #Cinema4D #Redshift #art #cg #cgart #scape #surrealism #RockinTuesday #TidesOutTuesday #ArtYear #ArtByHumans #CanadianArtist #BCArtist #BlueskyArtists

Not to my knowledge; the title comes from a twistor in the sense of Penrose. :)

A cloud of virtual sparks tracing circles in three-space against a blue-to-black twilight gradient. Each circle is a (1,1)-curve on a conformally-parametrized torus of rotation about the vertical axis. The palette runs from gold at the center to medium red at the outside.

The twistor flow on real 3-space, induced by unit complex scalar multiplication on the 3-sphere, in a warm palette.

www.diffgeom.com/product/roll...
www.diffgeom.com/product/canv...

#MathSky #MathArt

With slightly heavier lines the high-res image was suitable for my supplier. Now available:
www.diffgeom.com/product/roll...
www.diffgeom.com/product/canv...
#Math #MathArt

Thank you!

TBH, it's so different from (other prospective) poster images that I had mixed feelings. Your and others' positive responses mean a lot. :)

Thanks for your comment! To be honest, I half-expect blurring/low-res display to help bring out parts of the structure, such as the implicit tori. :)

A cloud of virtual sparks tracing circles in three-space against a blue-to-black twilight gradient. Each circle is a (1,1)-curve on a conformally-parametrized torus of rotation about the vertical axis. The palette runs from cyan at the center to purple at the outside.

The flow on real 3-space induced by unit complex scalar multiplication on the 3-sphere.

It's less ... focused ... than most of my mathematical portraits both visually and conceptually, but maybe more visceral and evocative?

#MathSky #MathArt

Mathematician Carol Karp was born 99 years ago today. Here research was in the area of infinitary logic, where infinitely long statements and infinitely long proofs are allowed. She wrote a foundational book on the subject in 1964.

#WomenInSTEM #MathSky #BookSky #HistSci 🧮

Photograph of flower-like mirror-polished sterling silver earrings, about 0.8in/20mm across, torus knots with seven-fold rotational symmetry.

These silver earrings in the Anemone family are a new design at Differential Geometry. The knotted band is a stylized representation of the complex 2/7-power function.

www.diffgeom.com/product/anem...

#MathSky #MathArt #Jewelry #3DPrinting

Photograph of a flower-like mirror-polished sterling silver pendant, about 1.2in/30mm across, with seven-fold rotational symmetry.

This silver pendant in the Anemone family is a new design at Differential Geometry. The knotted band is a stylized representation of the complex 2/7-power function.

www.diffgeom.com/product/anem...

#MathSky #MathArt #Jewelry #3DPrinting

Thank you for your supportive words, and for reposting! Separately, I'm happy the design appeals.

While <like>s are welcome, they're understandably stochastic. In any case, the most important validation comes from within. :)

Photograph of flower-like mirror-polished sterling silver earrings, about 0.8in/20mm across, torus knots with seven-fold rotational symmetry.

These silver earrings in the Anemone family are a new design at Differential Geometry. The knotted band is a stylized representation of the complex 2/7-power function.

www.diffgeom.com/product/anem...

#MathSky #MathArt #Jewelry #3DPrinting

Photograph of a flower-like mirror-polished sterling silver pendant, about 1.2in/30mm across, with seven-fold rotational symmetry.

This silver pendant in the Anemone family is a new design at Differential Geometry. The knotted band is a stylized representation of the complex 2/7-power function.

www.diffgeom.com/product/anem...

#MathSky #MathArt #Jewelry #3DPrinting

Also available dark on light:

www.diffgeom.com/product/post...

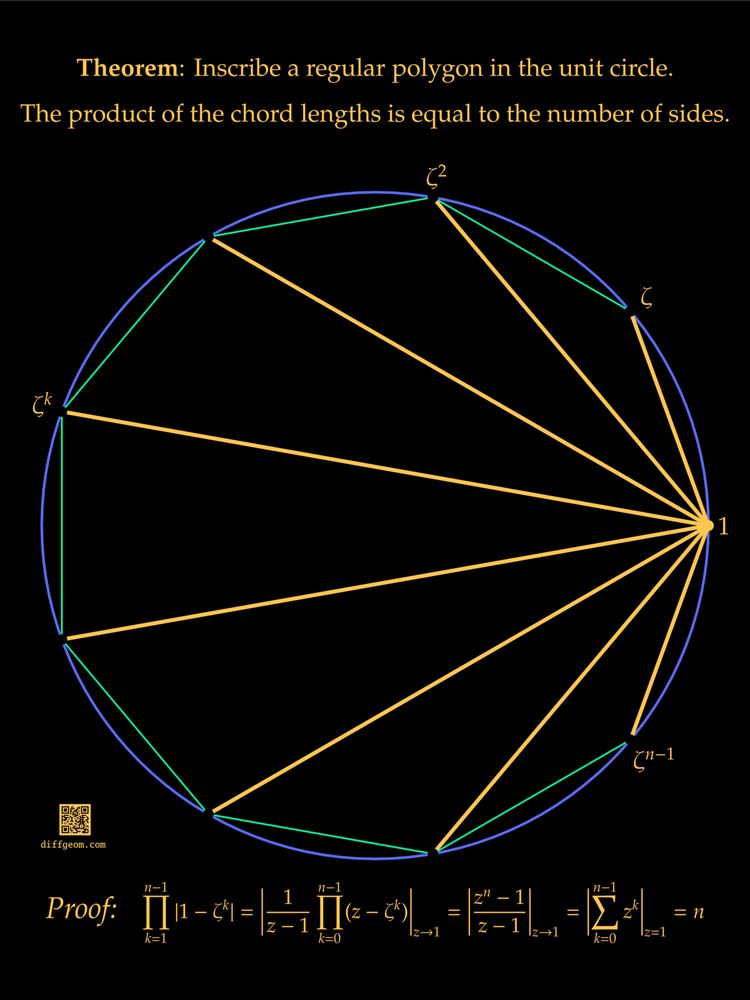
A diagram illustrating the theorem: Inscribe a regular polygon in the unit circle. The product of the chord lengths to a fixed vertex is equal to the number of sides. The circle is blue, the polygon green, and a family of chords to one vertex is gold. The vertices are labeled as complex roots of unity. A four-line proof is given.

Inscribe a regular n-gon in the unit circle. The product of the chord lengths from one vertex to the others is n, the number of sides. Most of my poster and T-shirt designs have no words or symbols. Sometimes an exception is in order.

www.diffgeom.com/product/post...

#MathSky #MathArt #ITeachMath

I miss #cohost

Hadn't seen this (thank you!), but did remember the famous (and award-winning) video by Douglas Arnold and Jonathan Rogness about conformal transformations of the plane (really, the sphere) that includes inversion: www-users.cse.umn.edu/~arnold/moeb...