Andrea Perin

On the Ability of Deep Networks to Learn Symmetries from Data: A Neural Kernel Theory Symmetries (transformations by group actions) are present in many datasets, and leveraging them holds significant promise for improving predictions in machine learning. In this work, we aim to underst...

Thanks for reading this thread until the end! For more, find the paper here: arxiv.org/abs/2412.11521

Since finite width deep networks are not kernel-analog, we can't discard the possibility that they might learn symmetries in some cases (grokking or other mysterious phenomena). We don't observe them to succeed empirically in any of our experiments though.

LIMITATIONS: Our results only apply to conventional architectures (MLPs, CNNs) trained with supervision, so we can't speak to other training procedures such as SSL, auto-encoding, meta-learning, and other architectures (e.g., we haven't studied the ViT kernel in detail).

In conclusion: we develop a theory for why deep nets lack a mechanism for generalization on datasets containing symmetries that have not been embedded in the architecture in advance. Our theory explains previous empirical results on the brittleness of deep learning.

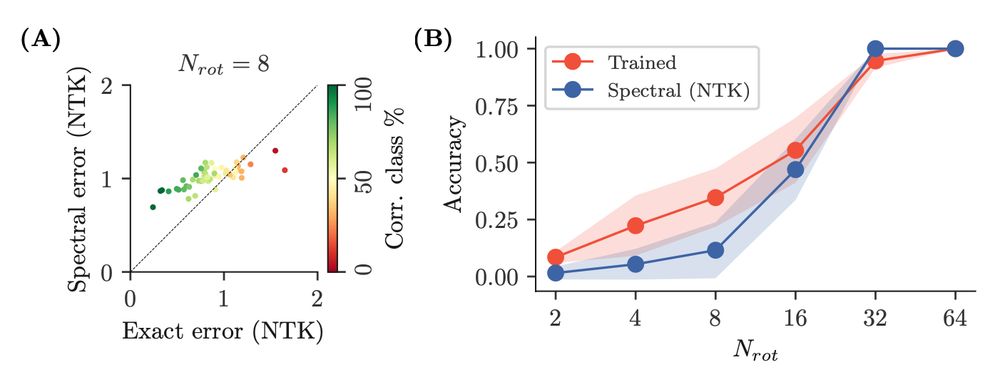
Finally, our theory recapitulates the behavior of finite width networks trained on a large subsection of MNIST, where specific rotations are held out during training for specific digit classes.

However, note that equivariant strategies rely on knowing the symmetry of the problem in advance. For complex symmetries in real world datasets, this may not always be the case.

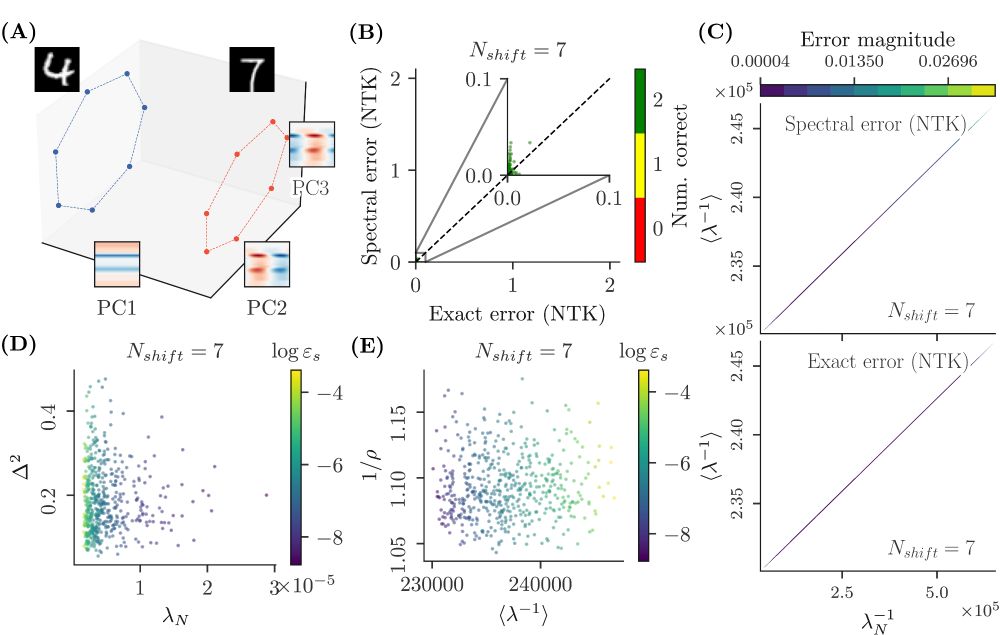
Regarding equivariant architectures, we recover the classical result that if the network architecture is invariant to the symmetry of interest, it will correctly generalize on the missing poses (because the orbits collapse in kernel space).

We conclude that deep networks are not specifically equipped to deal with symmetries. They see the two classes as two blobs to separate, and the task is easier if the blobs are compact and well separated in input space already.

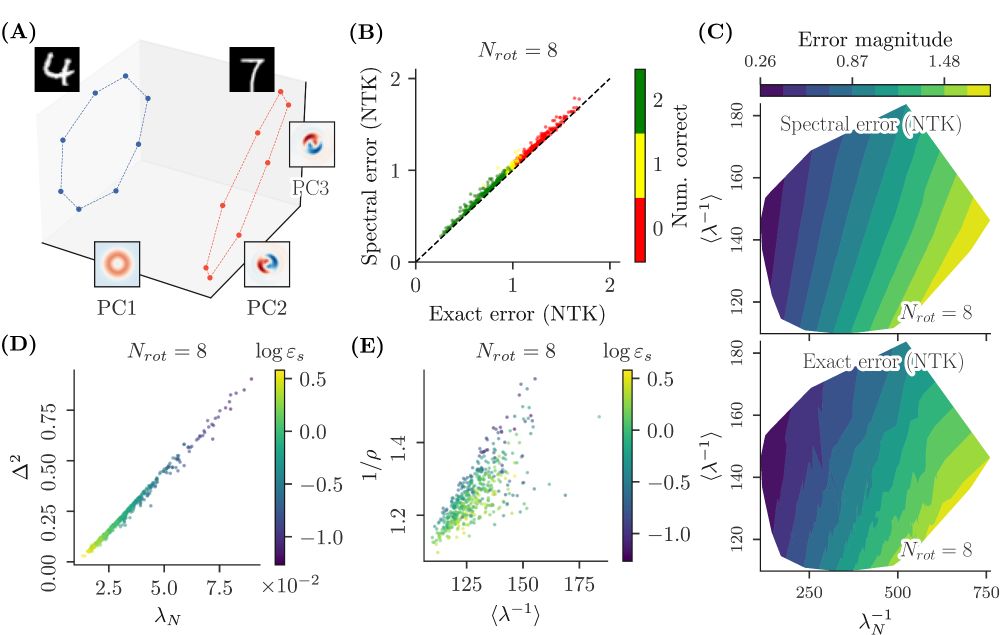
Our theory also applies to neural networks with various architectures (MLPs and CNNs), applied to pairs of rotation orbits of MNIST, in the kernel regime. Here too, correct generalization can be seen as a simple SNR: how distinct the classes are vs. how non-local the symmetric structure is.

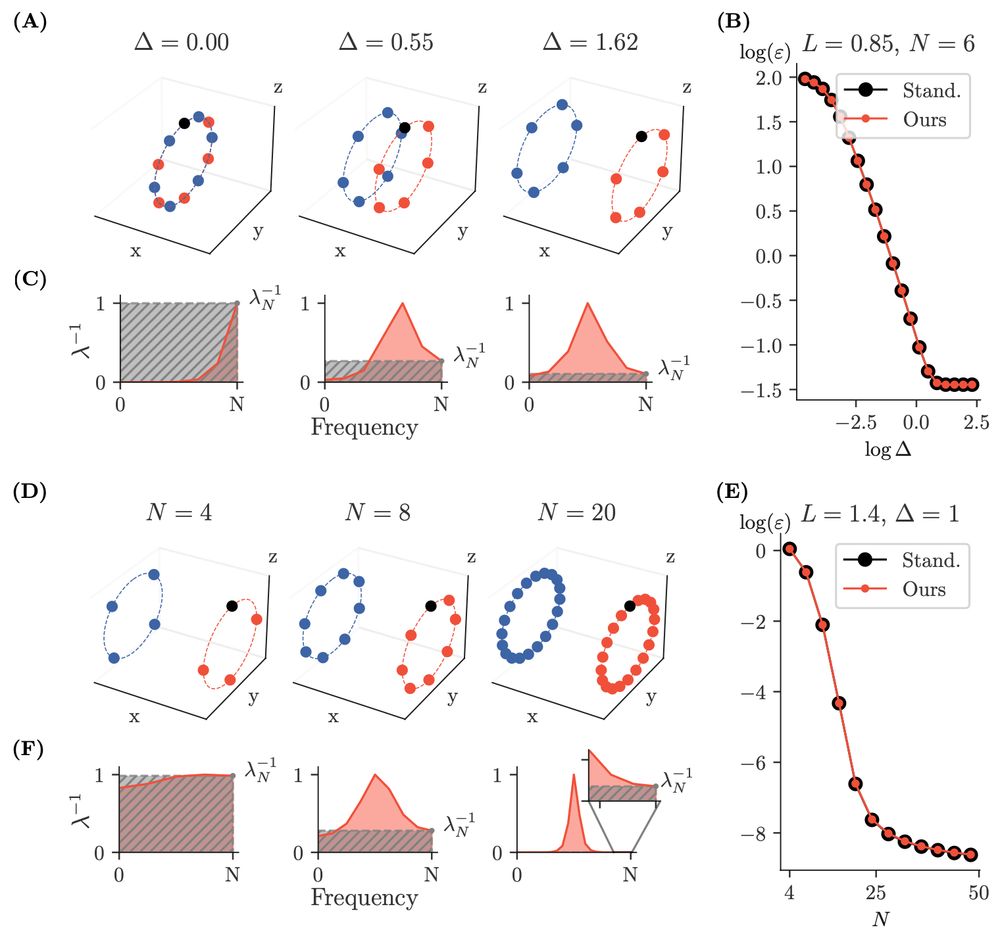
We derive geometric insights from the spectral formula, allowing us to understand when and why kernel methods fail to generalize on symmetric datasets. We find that, in the simplest cases, the numerator is prop. to class separation, while the denominator is prop. to the point density in an orbit.

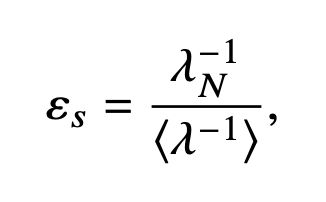
We derive a simple formula for the prediction error on a missing point, as a function of the (reciprocal) Fourier spectrum of the kernel matrix. We call it spectral error, and it is the ratio between the last reciprocal frequency and the average.

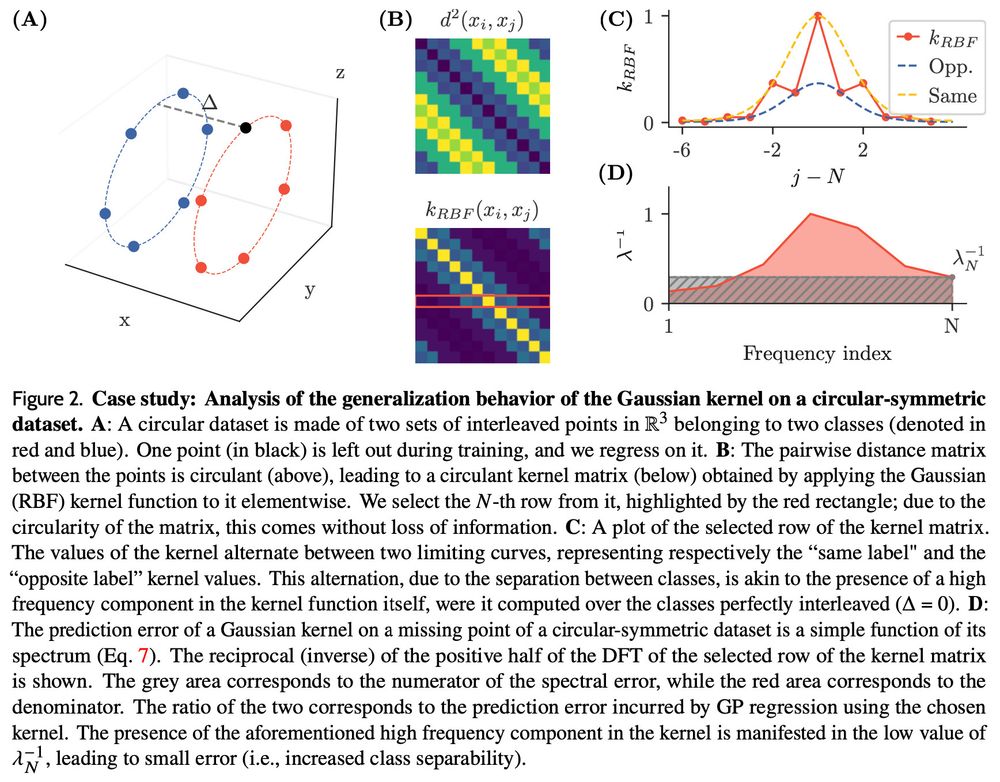
More precisely, our datasets are generated by the action of a cyclic group on two seed samples, forming two distinct classes. The kernel matrix on these datasets is circulant, and thus we can study the problem in Fourier space (here illustrated for the RBF kernel).

We work in the infinite width limit, where network inference becomes equivalent to kernel regression. We focus on simple group-cyclic datasets, which serve as a simple prototype for more complex (and realistic) symmetric datasets.

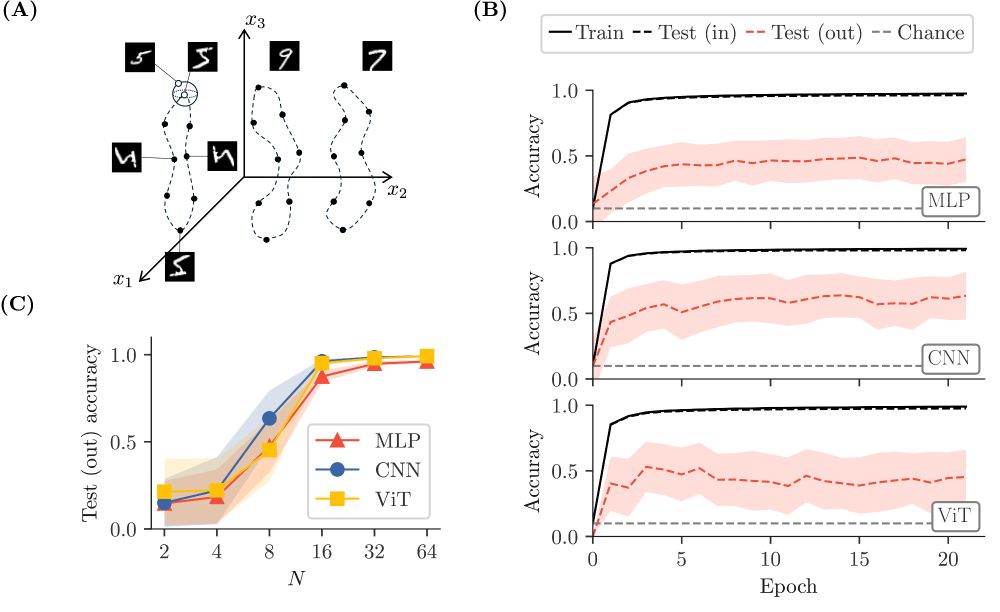
We empirically find that such generalization does not take place in general: for instance, networks cannot extrapolate unseen image rotations of MNIST digits, unless the number of sampled rotations is large. 𝘉𝘶𝘵 𝘸𝘩𝘺 𝘥𝘰 𝘯𝘦𝘵𝘸𝘰𝘳𝘬𝘴 𝘧𝘢𝘪𝘭?

This setup mimics real world scenarios, such as learning object pose invariance from limited examples. For instance, imagine a toddler seeing some objects in all possible poses (e.g., small toys), and other objects in some poses only (e.g., heavy furniture).

The question we ask is: if we expose a network to a dataset where the symmetries are only partially observed during training (for some classes, all possible transformations are seen, and for others, only some), should we expect generalization to the unseen classes and transformations?

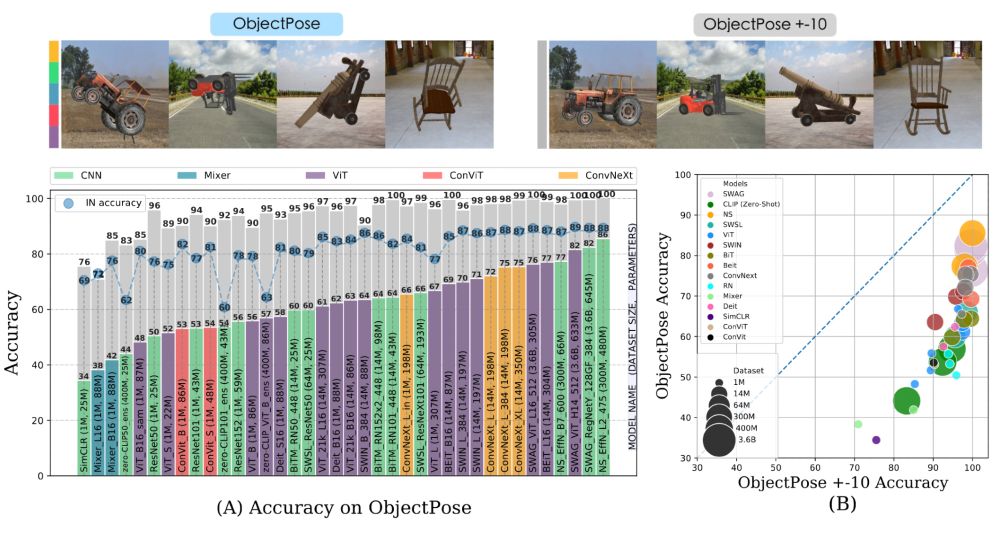
Deep networks tend to fare poorly on rare symmetric transformations, for instance objects seen in unusual poses. This has been observed empirically many times (see, for instance, Abbas and Deny, 2023 arxiv.org/abs/2207.08034).

On the Ability of Deep Networks to Learn Symmetries from Data: A Neural Kernel Theory Symmetries (transformations by group actions) are present in many datasets, and leveraging them holds significant promise for improving predictions in machine learning. In this work, we aim to underst...

Little is known about how deep networks interact with structure in data. An important aspect of this structure is symmetry (e.g., pose transformations). Here, we (w/ @stphtphsn.bsky.social) study the generalization ability of deep networks on symmetric datasets: arxiv.org/abs/2412.11521 (1/n)