The gifs didn't post properly 😅
Here is one showing the electron cloud in two stages: (1) the learning of electron density during training and (2) the predicted ground-state across conformations 😎
10.06.2025 22:06 — 👍 2 🔁 0 💬 0 📌 0

(9/9)⚡ Runtime efficiency
Self-refining training reduces total runtime up to 4 times compared to the baseline
and up to 2 times compared to the fully-supervised approach!!!
Less need for large pre-generated datasets — training and sampling happen in parallel.
10.06.2025 19:49 — 👍 2 🔁 0 💬 1 📌 0

(8/n) 🧪 Robust generalization
We simulate molecular dynamics using each model’s energy predictions and evaluate accuracy along the trajectory.
Models trained with self-refinement stay accurate even far from the training distribution — while baselines quickly degrade.
10.06.2025 19:49 — 👍 1 🔁 0 💬 1 📌 0

(7/n) 📊 Performance under data scarcity
Our method achieves low energy error with as few as 25 conformations.
With 10× less data, it matches or outperforms fully supervised baselines.
This is especially important in settings where labeled data is expensive or unavailable.
10.06.2025 19:49 — 👍 1 🔁 0 💬 1 📌 0

(6/n) This minimization leads to Self-Refining Training:
🔁 Use the current model to sample conformations via MCMC
📉 Use those conformations to minimize energy and update the model
Everything runs asynchronously, without need for labeled data and minimal number of conformations from a dataset!
10.06.2025 19:49 — 👍 1 🔁 0 💬 1 📌 0

(5/n) To get around this, we introduce a variational upper bound on the KL between any sampling distribution q(R) and the target Boltzmann distribution.
Jointly minimizing this bound wrt θ and q yields
✅ A model that predicts the ground-state solutions
✅ Samples that match the ground true density
10.06.2025 19:49 — 👍 2 🔁 0 💬 1 📌 0

(4/n) With an amortized DFT model f_θ(R), we define the density of molecular conformations as the
Boltzmann distribution
This isn't a typical ML setup because
❌ No samples from the density - can’t train a generative model
❌ No density - can’t sample via Monte Carlo!
10.06.2025 19:49 — 👍 1 🔁 0 💬 1 📌 0

(3/n) DFT offers a scalable solution to the Schrödinger equation but must be solved independently for each geometry by minimizing energy wrt coefficients C for a fixed basis.
This presents a bottleneck for MD/sampling.
We want to amortize this - train a model that generalizes across geometries R.
10.06.2025 19:49 — 👍 2 🔁 0 💬 1 📌 0
GitHub - majhas/self-refining-dft
Contribute to majhas/self-refining-dft development by creating an account on GitHub.
(2/n) This work is the result of an amazing collaboration with @fntwin.bsky.social Hatem Helal @dom-beaini.bsky.social @k-neklyudov.bsky.social
10.06.2025 19:49 — 👍 1 🔁 0 💬 1 📌 0
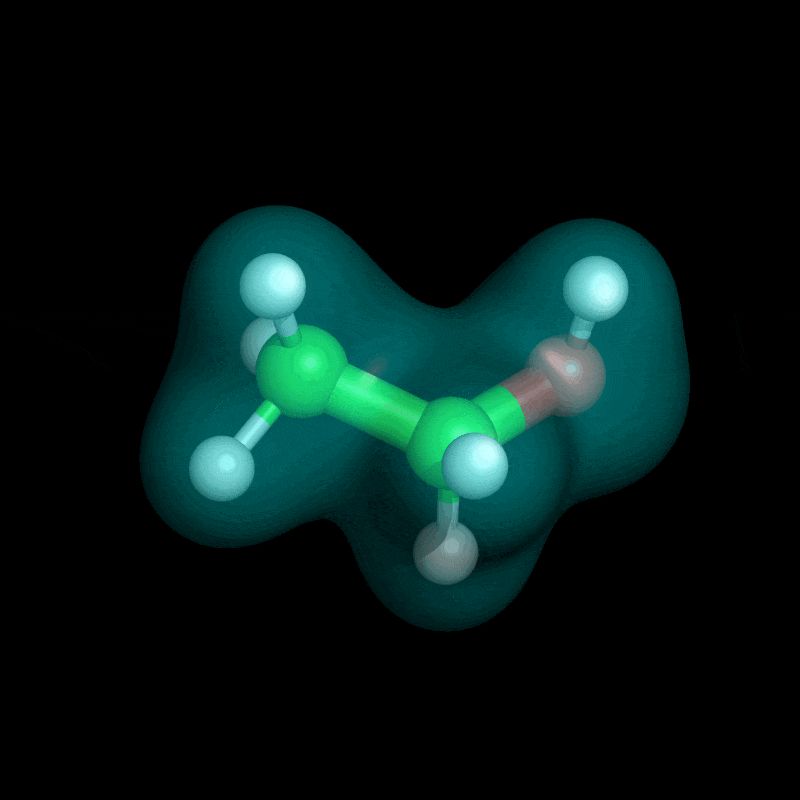
(1/n)🚨Train a model solving DFT for any geometry with almost no training data
Introducing Self-Refining Training for Amortized DFT: a variational method that predicts ground-state solutions across geometries and generates its own training data!
📜 arxiv.org/abs/2506.01225
💻 github.com/majhas/self-...
10.06.2025 19:49 — 👍 12 🔁 4 💬 1 📌 1

New preprint! 🧠🤖
How do we build neural decoders that are:
⚡️ fast enough for real-time use
🎯 accurate across diverse tasks
🌍 generalizable to new sessions, subjects, and even species?
We present POSSM, a hybrid SSM architecture that optimizes for all three of these axes!
🧵1/7
06.06.2025 17:40 — 👍 54 🔁 24 💬 2 📌 8
🧵(1/7) Have you ever wanted to combine different pre-trained diffusion models but don't have time or data to retrain a new, bigger model?
🚀 Introducing SuperDiff 🦹♀️ – a principled method for efficiently combining multiple pre-trained diffusion models solely during inference!
28.12.2024 14:32 — 👍 44 🔁 7 💬 1 📌 4

🔊 Super excited to announce the first ever Frontiers of Probabilistic Inference: Learning meets Sampling workshop at #ICLR2025 @iclr-conf.bsky.social!
🔗 website: sites.google.com/view/fpiwork...
🔥 Call for papers: sites.google.com/view/fpiwork...
more details in thread below👇 🧵
18.12.2024 19:09 — 👍 84 🔁 19 💬 2 📌 3
Now you can generate equilibrium conformations for your small molecule in 3 lines of code with ET-Flow! Awesome effort put in by @fntwin.bsky.social!
12.12.2024 16:37 — 👍 13 🔁 3 💬 0 📌 1
ET-Flow shows, once again, that equivariance is better than Transformer when physical precision matters!
come see us at @neuripsconf.bsky.social !!
07.12.2024 15:57 — 👍 6 🔁 1 💬 0 📌 0
Excited to share our work! I had a wonderful time collaborating with these brilliant people
07.12.2024 16:01 — 👍 4 🔁 0 💬 0 📌 0
NeuroAI at McGill University & Mila
MSc Student in NeuroAI @ McGill & Mila
w/ Blake Richards & Shahab Bakhtiari
UofT CompSci PhD Student in Alán Aspuru-Guzik's #matterlab and Vector Institute | prev. Apple
Incoming Assistant Prof, University of Alberta. Research Fellow at Amii. Currently, postdoc fellow the Broad Institute.
Computational Materials Scientist, Istanbul Technical University, Türkiye
@itu1773.bsky.social
phd student @geneva, ML+physics
https://balintmate.github.io
machine learning drug discovery scientist @ iambic tx | neuralplexer developer
computational biophysicist, glycoscientist, feminist, jewish, lover of sufjan stevens. she/they 🏳️🌈 ✡︎
📍 sf/nyc
Removing barriers to computational drug discovery one bit at a time. Associate Professor in Computational and Systems Biology at the University of Pittsburgh.
https://bits.csb.pitt.edu/
DL × Computational Physics: Diffusion/Flow Matching for molecular dynamics, statistical physics for DL and vice versa! Cellular automata hobbyist 👾 Covino Lab
PhD Student at MPI-IS working on ML for Gravitational Waves | #MLforPhysics #SBI
https://www.annalenakofler.com
Associate Professor at Chalmers. AI for molecular simulation and inverse design. WASP Fellow. ELLIS Member. https://userpage.fu-berlin.de/solsson/
AI/ML for Science & DeepTech | PI of the AI for Materials Lab | Prof. of Physics at UAM. https://bravoabad.substack.com/
Professor of Theoretical Chemistry @sorbonne-universite.fr & Director @lct-umr7616.bsky.social| Co-Founder & CSO @qubit-pharma.bsky.social | (My Views)
https://piquemalresearch.com | https://tinker-hp.org
Theoretical Chemistry research group @lct-umr7616.bsky.social, Sorbonne Université & CNRS| Led by Prof. Piquemal (@jppiquem.bsky.social)|
#compchem #HPC #MachineLearning #quantumcomputing
Website: https://piquemalresearch.com
Research scientist at Amazon. I studied at Mila during my Ph.D. and focused on understanding why AI discriminates based on gender and race; and how to measure/fix that.
A PhD student in Biophysics @JHU. Interested in proteins and deep learning.
PhD Student @CMUPittCompBio.bsky.social / @SCSatCMU.bsky.social
Interested in ML for science/Compuational drug discovery/AI-assisted scientific discovery 🤞
from 🇱🇰🫶 https://new.ramith.fyi
BME & CS @Duke | Protein Designer @ColumbiaMed
biology + computers + a leavening of snark | 👨👨👧👧🏳️🌈| nanomedicine | cancer genomics 🧬 | ML | biomaterials | #compchem #matsky #chemsky #ai4science #materialsinformatics #md | startups | @Cal 🐻 @Stanford @UniversityOfOxford @OxfordNano (swimsf on the Bad Place)
Ph.D. Student @ Mila Québec 🍁🤖🧗♀️
Machine learning, optimization
M.Sc. @ UBC Vancouver
https://tianyuehz.github.io/












