Bálint Máté

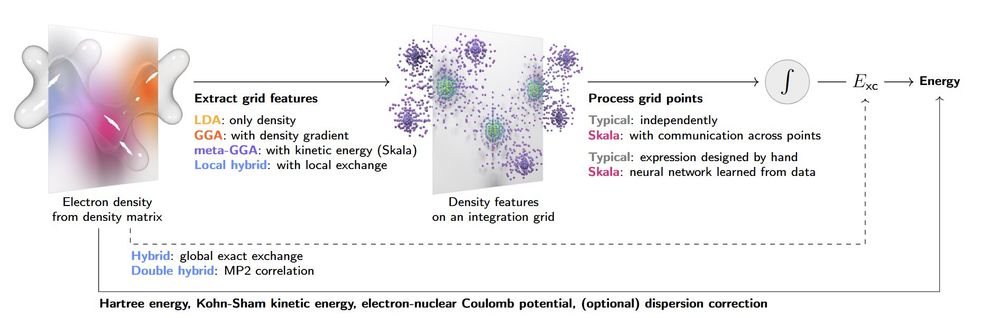
🚀 After two+ years of intense research, we’re thrilled to introduce Skala — a scalable deep learning density functional that hits chemical accuracy on atomization energies and matches hybrid-level accuracy on main group chemistry — all at the cost of semi-local DFT ⚛️🔥🧪🧬

Finally, we also look at what happens if we predict the hydration free energy of methane using the potential that was trained on water (and vice versa). (10/10)

The approach is tested on the estimation of hydration free energies of rigid water and methane (LJ + Coulomb interactions). We find good agreement with experimental reference values. (9/n)

Target Score Matching Denoising Score Matching estimates the score of a noised version of a target distribution by minimizing a regression loss and is widely used to train the popular class of Denoising Diffusion Models. A...

We then parametrize the interpolating potential with a neural network and train it to be the equilibrium potential corresponding to the samples.
Since the endpoint Hamiltonians are also available, we do this with target score matching. (8/n)

arxiv.org/abs/2402.08667

Flow Matching for Generative Modeling We introduce a new paradigm for generative modeling built on Continuous Normalizing Flows (CNFs), allowing us to train CNFs at unprecedented scale. Specifically, we present the notion of Flow Matching...

We do this by simply taking the geodesic interpolation between pairs of samples from the endpoint distributions. This is, of course, inspired by flow matching/stochastic interpolants. (7/n)

arxiv.org/abs/2210.02747
arxiv.org/abs/2303.08797

In this work, we go the other way around, and define the interpolation by the sampling process of the intermediate densities. (6/n)

For TI, this means that we are free to choose one way of describing this interpolation, and the hard part is getting the other one. Usually one chooses the interpolation of potentials and performs simulations at a sequence of intermediate potentials to obtain samples. (5/n)

Note that (1) and (2) define the same object, a one-parameter family of probability densities interpolating between the endpoint Boltzmann distributions. (4/n)

Thus, to numerically estimate the free-energy difference, two things are necessary: (1) an interpolating family of potentials and (2) samples from the Boltzmann densities of the intermediate potentials to estimate the expectation value in the integrand. (3/n)

Thermodynamic Integration (TI) computes the free energy difference between two potentials as an integral over a coupling variable parametrising an interpolation between the two potentials. (2/n)

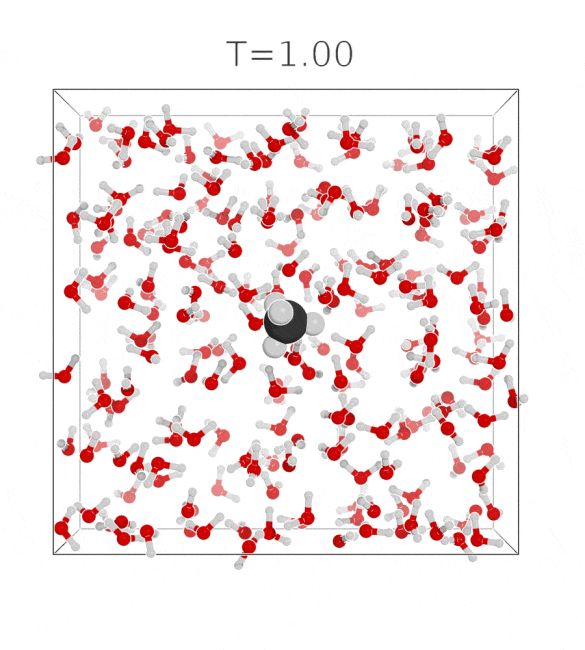
hello bluesky! we have a new preprint on solvation free energies:

tl;dr: We define an interpolating density by its sampling process, and learn the corresponding equilibrium potential with score matching. arxiv.org/abs/2410.15815

with @francois.fleuret.org and @tbereau.bsky.social
(1/n)