welp twitter's not working
hello bsky, how's everyone doing?
i haven't been here in a while, how many of my twitter circles are still using this thing?
monk
@monk.bsky.social
improver of circumstances
@monk.bsky.social
improver of circumstances
welp twitter's not working
hello bsky, how's everyone doing?
i haven't been here in a while, how many of my twitter circles are still using this thing?
yeah that's what i'm thinking, the blockchain idealism of immutability and append-only, but for communication in the real world that's just not a good idea
17.05.2023 10:19 — 👍 5 🔁 0 💬 0 📌 0ME AND WHO
14.05.2023 22:18 — 👍 8 🔁 0 💬 1 📌 0hmm yeah probably way fewer views than i'd have with the same number of followers on twitter
still, getting 0 likes is weird
weird that it's normal for me to get 0 likes on a skeet here
on twitter that has literally never happened once i hit like 200 followers

welp that didn't work out
mfw
lovely
03.05.2023 14:56 — 👍 0 🔁 0 💬 0 📌 0
ok what about now
03.05.2023 14:56 — 👍 0 🔁 0 💬 1 📌 0reply threads now 10x more readable, thanks!!
03.05.2023 14:55 — 👍 2 🔁 0 💬 0 📌 0if there's wifi and conveniently placed electrical outlets i'd show up
03.05.2023 13:39 — 👍 2 🔁 0 💬 0 📌 0what form of answer do you expect?
if you ask "who is that person" and i say "that's my friend harry" and you say "but WHO is harry?", what am i supposed to answer? harry is harry, it's *a* particular person. tpot is tpot, it's *a* particular part of twitter
yeah i mean it will open a link in the browser
03.05.2023 09:46 — 👍 1 🔁 0 💬 0 📌 0i find it hilarious that jay was like "omg pls don't let the name skeets stick, anything but skeets" and then someone comes along and is like "why would jay decide to name them skeets, that's so strange"
but also i feel bad for the team a bit
they talked about bluesky on yesterday's episode of blocked and reported
"they named them 'skeets'... why would they do that, i don't get it"
priceless entertainment, 10/10

ok i see how it is
29.04.2023 23:09 — 👍 0 🔁 0 💬 1 📌 0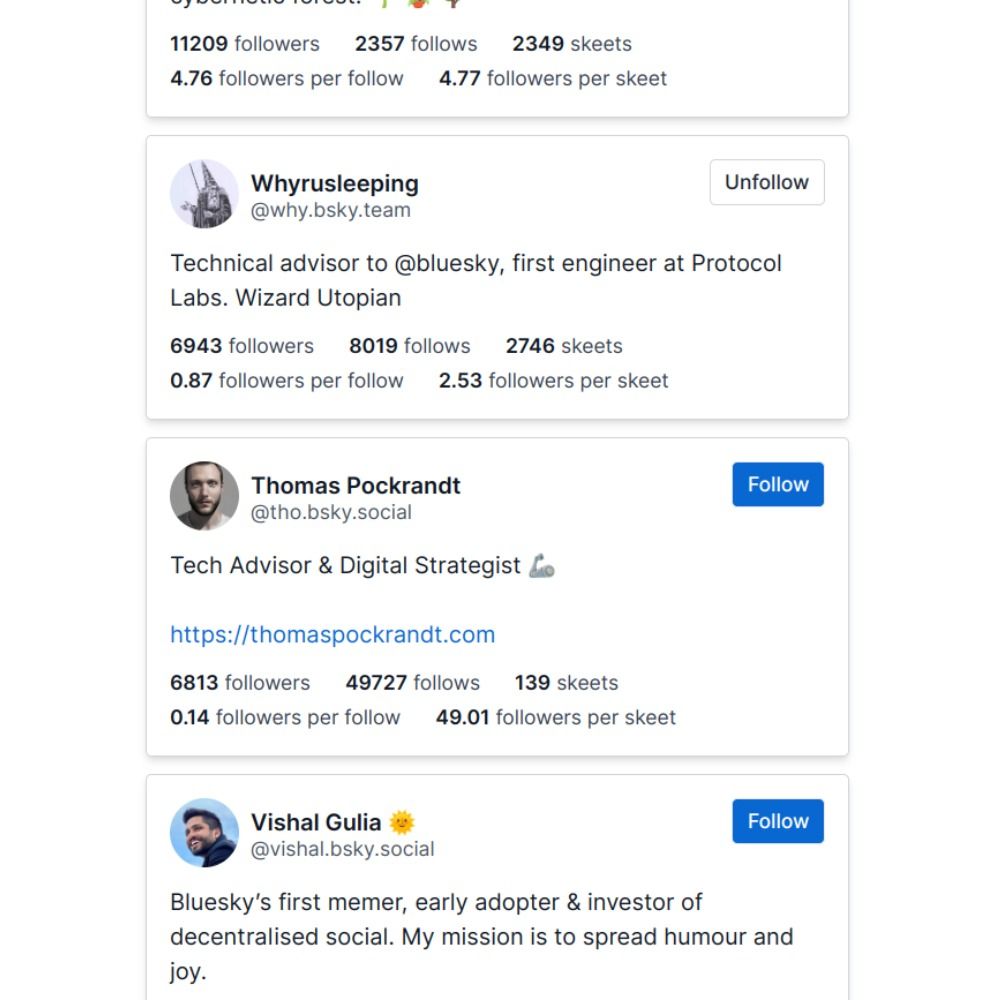
another update: follow and unfollow buttons
29.04.2023 20:38 — 👍 0 🔁 0 💬 1 📌 0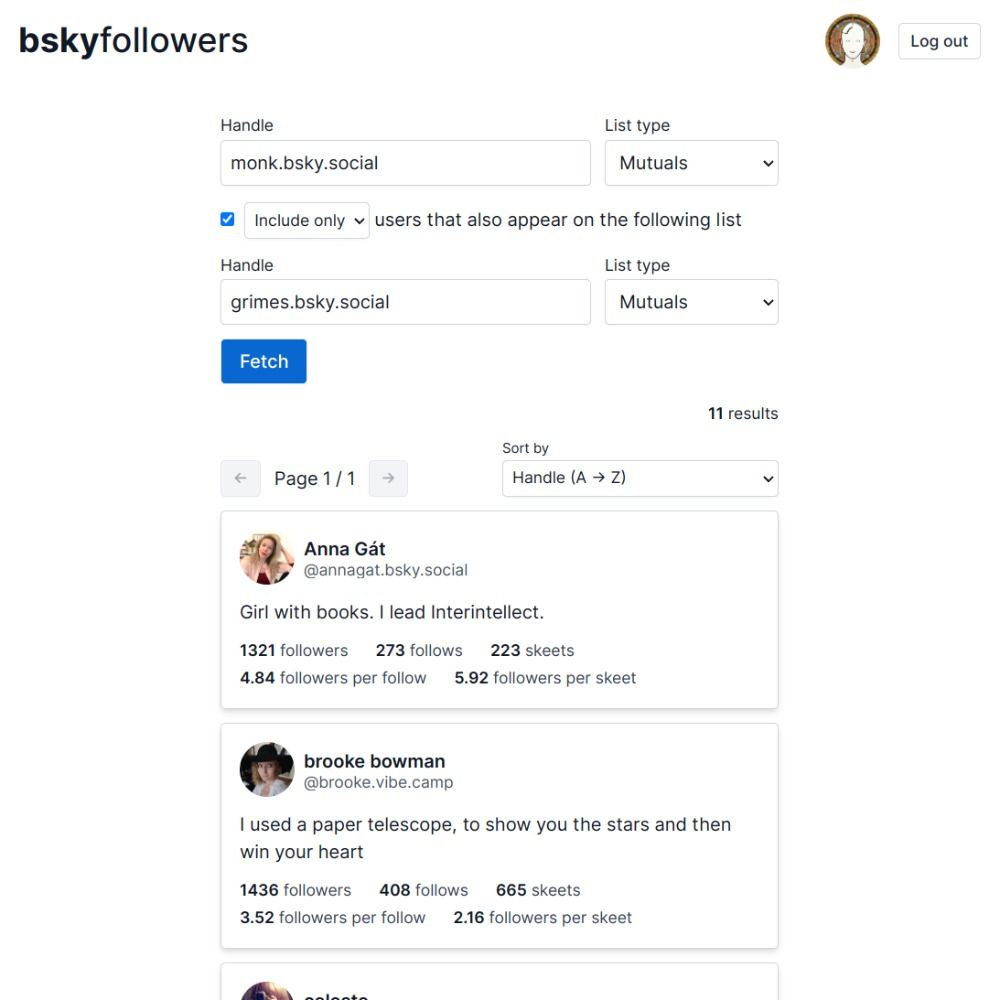
first enhancement: the option of combining two lists
i just used it to find moots from twitter that i wasn't yet following here by looking at people that my friends followed that i didn't
senpai notice me (bsky team)
29.04.2023 01:00 — 👍 1 🔁 0 💬 1 📌 0also i just noticed the original listfollowers doesn't work, did elon shut down the twitter API at last?
29.04.2023 00:32 — 👍 4 🔁 0 💬 1 📌 0as you can see i made it usable on mobile too this time
pls clap
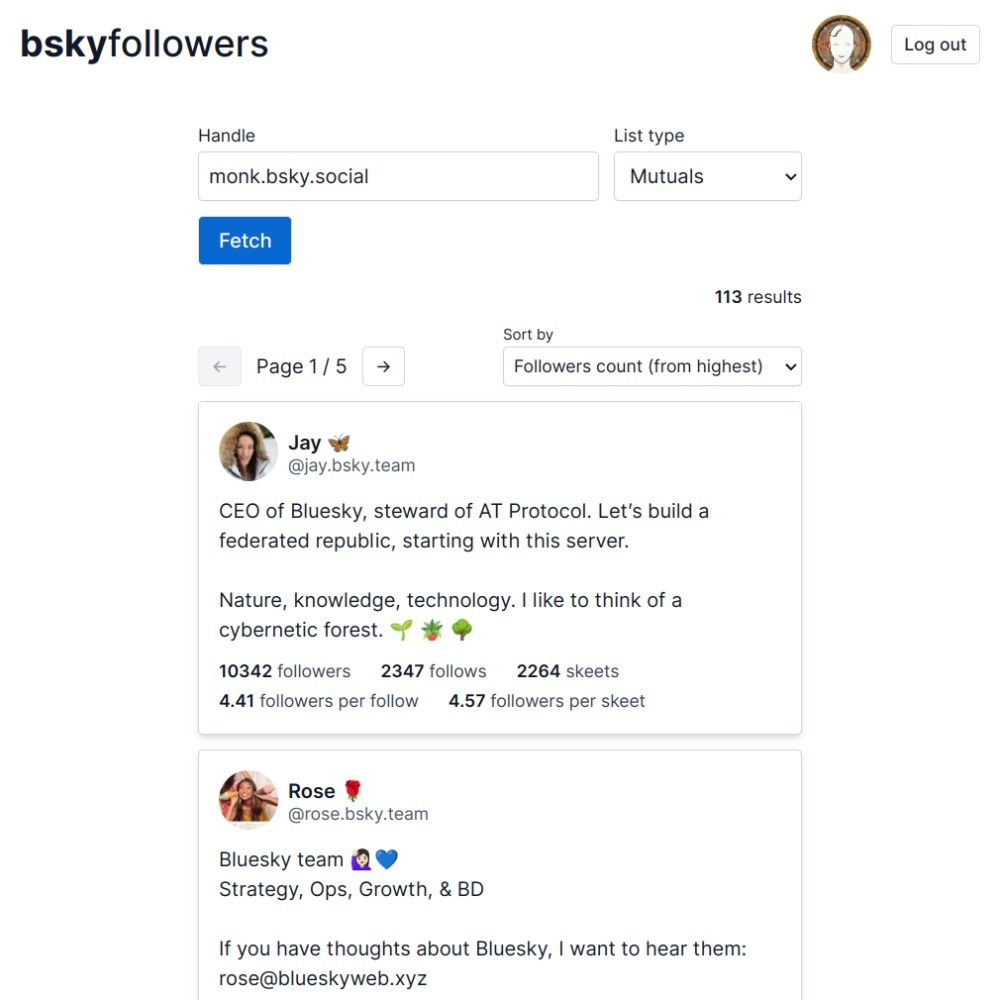
anyway
the most basic version of listfollowers for bsky is out now
https://bskyfollowers.netlify.app/
there's no search, export, combining 2 lists etc, that's all coming
also no error handling bc there's no docs for the API, idk what errors can even happen
try it out, if it crashes let me know
today i mostly just played with tailwind and created silly little layouts and silly little components and silly little color palettes
next time i should do some actual programming
ah, the thing i mentioned in the QT, ie the same thing i built on twitter api before, ie a website that allows you to fetch a list of someone's follows or followers, search/sort/filter through them, save to json/csv, intersect or subtract two users' lists etc
23.04.2023 08:41 — 👍 0 🔁 0 💬 0 📌 0oh you mean like web vs mobile? web
22.04.2023 23:03 — 👍 0 🔁 0 💬 0 📌 0are you asking about the features or the tech stack?
22.04.2023 23:02 — 👍 0 🔁 0 💬 2 📌 0on bsky the logic itself is much faster to code because there's no rate limits to optimize around and error-handle
so much thinking on listfollowers went into working with the rate limits
here i just… fetch the data and show it
also everyone has like 500 followers anyway rn
started one week later but finally under way
today i fairly quickly discarded the idea of making my own backend right off the bat
i'll start frontend only to ship something quick; afterwards i can fuck around w session cookies and bullshit like that
most of the work is UI which won't go to waste
there's an android app?? i didn't find anything searching the app store so i assumed there isn't
22.04.2023 16:23 — 👍 0 🔁 0 💬 1 📌 0"the densely connected subgraph"
i like this
on social localism
22.04.2023 16:12 — 👍 2 🔁 0 💬 0 📌 0