Dimitri Meunier

Solenne Gaucher, la mathématicienne qui sort le genre de l’équation « La Relève ». Chaque mois, « Le Monde Campus » rencontre un jeune qui bouscule les normes dans son domaine. A 31 ans, la docteure en mathématiques s’attaque aux biais algorithmiques de l’intelligence artificielle et a reçu en 2024 un prix pour ses travaux.

Solenne Gaucher, la mathématicienne qui sort le genre de l’équation

Congrats !

AISTATS 2026 will be in Morocco!

Gaussian Processes and Reproducing Kernels: Connections and Equivalences This monograph studies the relations between two approaches using positive definite kernels: probabilistic methods using Gaussian processes, and non-probabilistic methods using reproducing kernel Hilb...

We've written a monograph on Gaussian processes and reproducing kernel methods (with @philipphennig.bsky.social, @sejdino.bsky.social and Bharath Sriperumbudur).

arxiv.org/abs/2506.17366

I have been looking at the draft for a while, I am surprised you had a hard time publishing it, it is a super cool work! Will it be included in the TorchDR package ?

Distributional Reduction paper with H. Van Assel, @ncourty.bsky.social, T. Vayer , C. Vincent-Cuaz, and @pfrossard.bsky.social is accepted at TMLR. We show that both dimensionality reduction and clustering can be seen as minimizing an optimal transport loss 🧵1/5. openreview.net/forum?id=cll...

Dimitri Meunier, Antoine Moulin, Jakub Wornbard, Vladimir R. Kostic, Arthur Gretton
Demystifying Spectral Feature Learning for Instrumental Variable Regression
https://arxiv.org/abs/2506.10899

Very much looking forward to this ! 🙌 Stellar line-up

new preprint with the amazing @lviano.bsky.social and @neu-rips.bsky.social on offline imitation learning! learned a lot :)

when the expert is hard to represent but the environment is simple, estimating a Q-value rather than the expert directly may be beneficial. lots of open questions left though!

TL;DR:

✅ Theoretical guarantees for nonlinear meta-learning
✅ Explains when and how aggregation helps
✅ Connects RKHS regression, subspace estimation & meta-learning

Co-led with Zhu Li 🙌, with invaluable support from @arthurgretton.bsky.social, Samory Kpotufe.

Even with nonlinear representation you can estimate the shared structure at a rate improving in both N (tasks) and n (samples per task). This leads to parametric rates on the target task!⚡

Bonus: for linear kernels, our results recover known linear meta-learning rates.

Short answer: Yes ✅

Key idea💡: Instead of learning each task well, under-regularise per-task estimators to better estimate the shared subspace in the RKHS.

Even though each task is noisy, their span reveals the structure we care about.

Bias-variance tradeoff in action.

Our paper analyses a meta-learning setting where tasks share a finite dimensional subspace of a Reproducing Kernel Hilbert Space.

Can we still estimate this shared representation efficiently — and learn new tasks fast?

Most prior theory assumes linear structure: All tasks share a linear representation, and task-specific parts are also linear.

Then: we can show improved learning rates as the number of tasks increases.

But reality is nonlinear. What then?

Meta-learning = using many related tasks to help learn new ones faster.

In practice (e.g. with neural nets), this usually means learning a shared representation across tasks — so we can train quickly on unseen ones.

But: what’s the theory behind this? 🤔

Nonlinear Meta-Learning Can Guarantee Faster Rates Many recent theoretical works on \emph{meta-learning} aim to achieve guarantees in leveraging similar representational structures from related tasks towards simplifying a target task. The main aim of ...

🚨 New paper accepted at SIMODS! 🚨
“Nonlinear Meta-learning Can Guarantee Faster Rates”

arxiv.org/abs/2307.10870

When does meta learning work? Spoiler: generalise to new tasks by overfitting on your training tasks!

Here is why:
🧵👇

Dimitri Meunier, Zikai Shen, Mattes Mollenhauer, Arthur Gretton, Zhu Li
Optimal Rates for Vector-Valued Spectral Regularization Learning Algorithms
https://arxiv.org/abs/2405.14778

Mattes Mollenhauer, Nicole M\"ucke, Dimitri Meunier, Arthur Gretton: Regularized least squares learning with heavy-tailed noise is minimax optimal https://arxiv.org/abs/2505.14214 https://arxiv.org/pdf/2505.14214 https://arxiv.org/html/2505.14214

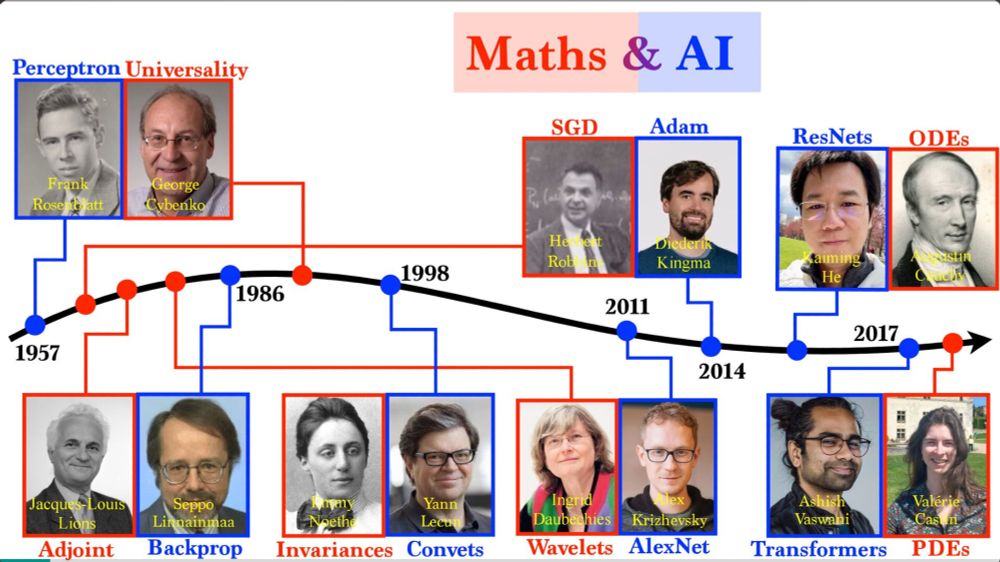
I have updated my slides on the maths of AI by an optimal pairing between AI and maths researchers ... speakerdeck.com/gpeyre/the-m...

Optimal Transport for Machine Learners Optimal Transport is a foundational mathematical theory that connects optimization, partial differential equations, and probability. It offers a powerful framework for comparing probability distributi...

I have cleaned a bit my lecture notes on Optimal Transport for Machine Learners arxiv.org/abs/2505.06589

Gabriel Peyr\'e
Optimal Transport for Machine Learners
https://arxiv.org/abs/2505.06589

New ICML 2025 paper: Nested expectations with kernel quadrature.

We propose an algorithm to estimate nested expectations which provides orders of magnitude improvements in low-to-mid dimensional smooth nested expectations using kernel ridge regression/kernel quadrature.

arxiv.org/abs/2502.18284

Great talk by Aapo Hyvärinen on non linear ICA at AISTATS 25’!

Density Ratio-based Proxy Causal Learning Without Density Ratios 🤔

at #AISTATS2025

An alternative bridge function for proxy causal learning with hidden confounders.
arxiv.org/abs/2503.08371
Bozkurt, Deaner, @dimitrimeunier.bsky.social, Xu

YouTube video by ML New Papers Interview of Statistics and ML Expert - Pierre Alquier

Link to the video: youtu.be/nLGBTMfTvr8?...

🤩 c’était super de te revoir Pierre!

Dinner in Siglap yesterday evening with the members of the ABI team & friends who are attending ICLR.

Optimality and Adaptivity of Deep Neural Features for Instrumental Variable Regression
#ICLR25

openreview.net/forum?id=ReI...

NNs
✨better than fixed-feature (kernel, sieve) when target has low spatial homogeneity,
✨more sample-efficient wrt Stage 1

Kim, @dimitrimeunier.bsky.social, Suzuki, Li

Super, c'est noté, merci!

Félicitations ! Je cherchais justement des bornes non iid pour KME, ça tombe à point :)