Lipsum.dev

Wait, Euclid geometry, or the theory of algebraically closed fields of characteristic 0 aren't powerful theories?

Je l'ai eu en cours à l'X, j'ai le souvenir d'un authentique amoureux de la transmission de connaissance.

On peut donc s'interroger sur la sincérité du discours de tous ces gens qui disent vouloir "défendre les sciences" (je n'ai pas d'avis sur le pesticide en question par ailleurs, c'est assez difficile d'accéder à de l'information de qualité)

En tout cas, ce sujet mobilise plus que la défense d'un lieu dédié à la promotion des sciences (le Palais de la Découverte), dont la pétition qui est en ligne depuis plus longtemps a recueilli beaucoup moins de signatures, et n'a pas semblé agité les écolos-à-la-mode.

...mais que comme on n'apporte pas cette énergie (contrairement à un radiateur qui la puise intégralement du réseau électrique <- c'est là qu'il faut insister) on a malgré tout un bien meilleur rendement.

Dès lors, on pourrait dire que l'énergie à fournir à la pompe à chaleur est celle nécessaire à aller "contre" le sens "facile" de transfert de l'énergie (de l'intérieur vers l'extérieur en hivers)...

Sinon, concernant la pompe à chaleur (en mode chauffage), je pense que le point clef à vulgariser serait qu'une pompe à chaleur est plus efficace car elle vient prendre de l'énergie qui existe déjà (ce qui surprendra les gens car ils imaginent que comme il fait froid dehors il n'y a rien à prendre).

Ah je pense pas qu'il faille le mentionner à ce niveau, on est d'accord. Je dis juste que c'est *le* point qui posera problème (à mon avis).

Très franchement, je ne suis pas certain que cette présentation soit si accessible. Il me semble que tant qu'on ne rentre pas dans une présentation via la physique statistique, l'entropie peut apparaître comme un truc « tombé du ciel » dont il est difficile de se faire une intuition.

Photo des 4 dés intransitifs de Bradley Efron (à l'Institut Henri Poincaré)

Tiens j'avais vu ça à l'Institut Henri Poincaré.

Image de Han Solo et Chewbacca passant en vitesse lumière à bord du Faucon Millenium. Les étoiles semblent s'écarter les unes des autres.

Dans la fameuse image ci-dessous, si l'on suppose que les étoiles sont à l'infini, on devrait donc les voir... se rapprocher du centre (pour des points à distances finies, cet effet est opposé à l'augmentation de l'écart angulaire).

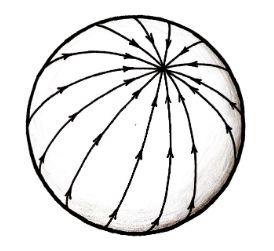
Image de la sphère de Poincaré illustrant une transformation de Möbius faisant converger les points vers le pôle nord.

En particulier, un « boost » dans une direction correspondant à un point P (ici le pôle nord) de la sphère est associé à une transformation qui fait converger les points *vers* P.

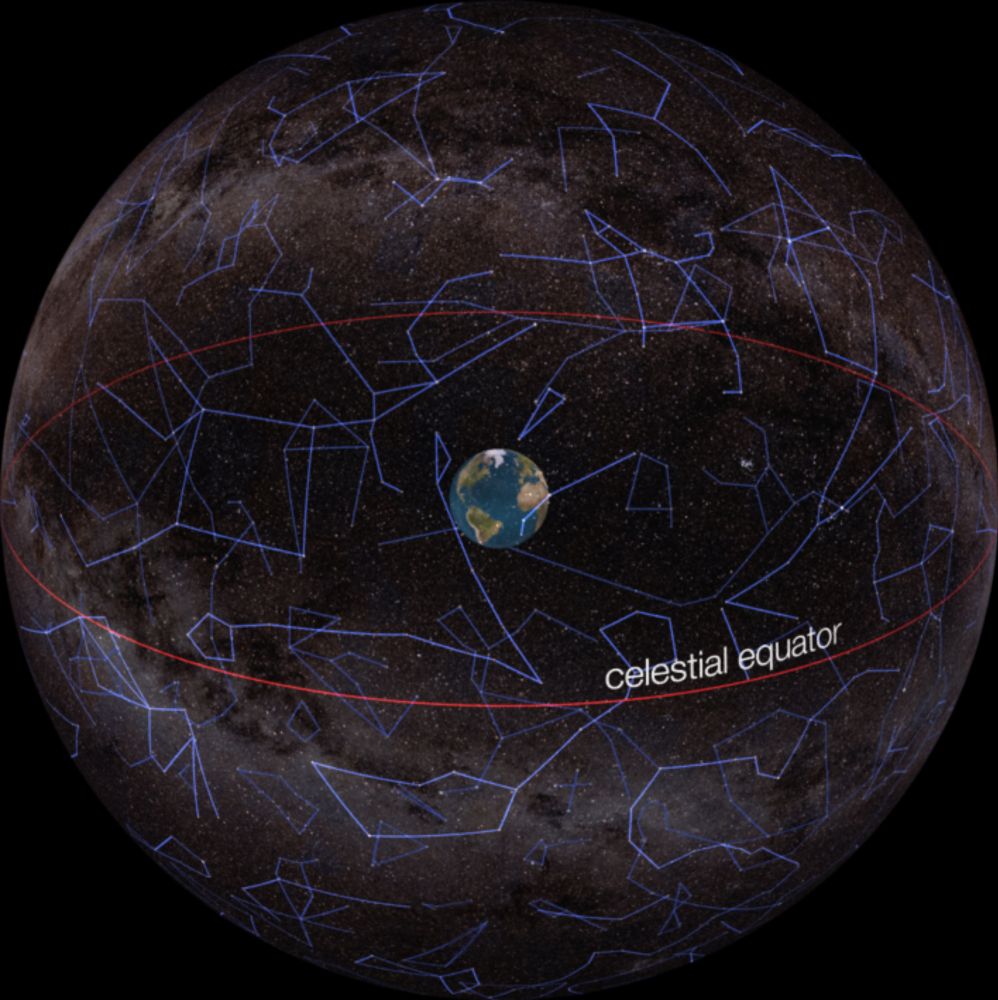
Celestial sphere - Wikipedia

On peut considérer cette sphère infinie comme la « sphère céleste » (en.wikipedia.org/wiki/Celesti...), et les transformations de Lorentz agissent dessus comme des transformations conformes (celles données par le groupe de Möbius).

Ce que le papier nous apprend, c'est que cette isomorphisme peut se voir de façon naturelle, en faisant agir le groupe de Lorentz sur une sphère associée à un paramétrage bien choisi de l'espace-temps, puis en faisant tendre le rayon de cette sphère vers l'infini.

En particulier, est mis en évidence l'isomorphisme entre :
* le groupe de Möbius (fr.wikipedia.org/wiki/Transfo...), qui agit sur la sphère unité (considérée comme une version compacte du plan complexe — la « sphère de Poincaré »)
* le groupe de Lorentz (en fait, la composante connexe de l'identité)

From the Lorentz Group to the Celestial Sphere In these lecture notes we review the isomorphism between the (connected) Lorentz group and the set of conformal transformations of the sphere. More precisely, after establishing the main properties of...

C'est ce que nous explique ce papier arxiv.org/abs/1508.00920 qui présente une étude détaillée (et mathématiquement rigoureuse) du groupe de Lorentz.

Image de Han Solo et Chewbacca passant en vitesse lumière à bord du Faucon Millenium.

Cette image serait-elle fausse !?! ⬇️

J'imagine ajouter un commentaire dans la base de code « Do not use this unless your argument corresponds to a total computable function! ».

(ludovicpatey.com/courses/comp...)

C'est vrai que, paradoxalement, cette discipline pourtant directement liée à l'informatique, semble très détachée des applications et plus proche de la philosophie (peut-être plus que beaucoup de branches des mathématiques).

Le bouquin de référence en français sur la calculabilité introduit le sujet par : « La calculabilité, via la compréhension qu’elle donne des objets incalculables, a obtenu des succès majeurs en fournissant un cadre formel pour l’étude de questions à la frontière entre science et philosophie. »

Après, pour un usage « dans la vraie vie » (dans un vrai langage de programmation, hors calculabilité), j'ai du mal à imaginer un cas où ce n'est pas la solution (c) qui est la seule naturelle.

En particulier, on peut donner à manger à la boîte noire un point quelconque de 2^ℕ, par exemple un où la « fonction (2^ℕ)^rec → ℕ calculable non bornée » serait contrainte à valoir l'infini — elle n'y est en fait pas définie puisque ce point n'est pas calculable.

Ce que je répondrais intuitivement (mais j'ai pas encore tout bien digéré), c'est que la classe des fonctions f: (2^ℕ)^rec → 2 est moins contrainte que celle des fonctions qui sont autorisées à prendre une fonction « boîte noire » p: ℕ -> 2 en argument.

Question bonus (pour les neuneus) : pourquoi ce qu'a expliqué @gro-tsen.bsky.social ci-dessus ne contredit pas l'existence de programmes comme ceux mentionnés dans math.andrej.com/2007/09/28/s... ?

Je mets ce lien pour les neuneus comme moi, qui détaille un peu plus la construction de l'arbre de Kleene évoqué au-dessus : math.andrej.com/wp-content/u...

Dans l'article math.andrej.com/2007/09/28/s..., on a `type Cantor = Natural -> Bit` et l'accès à cette fonction se fait donc déjà en « boîte noire ».

On est d'accord que le théorème susmentionné importe peu (pour montrer la correction du programme), ou je n'ai rien compris ?

« Ce qu’affirme le théorème de KLS, c’est que toute valeur F(g) calculée ne dépend, en fait, que d’un nombre fini de telles valeurs (...), et, finalement (...) peut être calculé par un algorithme qui n’a le droit d’accéder qu’à une boîte noire (...) » (perso.telecom-paristech.fr/madore/inf11...)

Concernant ton point ②, « l'omniscience de l'ensemble de Cantor {0,1}^ℕ » c'est quand-même assez différent du théorème KLS tel que tu l'as présenté non ? (je vois des histoires de continuité en commun, mais pas beaucoup plus, j'ai loupé quelque chose ?)

Lien vers le fil précédent : bsky.app/profile/lips...

Un résultat clef (que j'évoque en fin d'article) est le théorème de la base basse (en.wikipedia.org/wiki/Low_bas...).
Il faudra que j'essaie d'en comprendre la démonstration, qui est très technique...