Andrew Stacey

Ah, I think I inferred something you didn't imply - namely, that the meeting point of the semi-circle and quarter circle was needed to solve the rest of the puzzle.

Rather, it ends up being at the highest point *anyway*. Neat!

I'd be interested to see your reasoning here. What leads you to that conclusion?

Thanks for reposting - and confirming a solution!

I initially wondered if the intersections between the semi-circle and quarter circle were meant to be at the highest point on the semi-circle (this was before I thought I'd found a solution that didn't need the semi-circle).

(NB There's a link to the original post on twitter. I /presume/ that this is discussed there but I no longer have a twitter account so cannot follow links within twitter. So someone who still has such an account could just look it up. But, it'd be nicer to have that discussion here not there!)

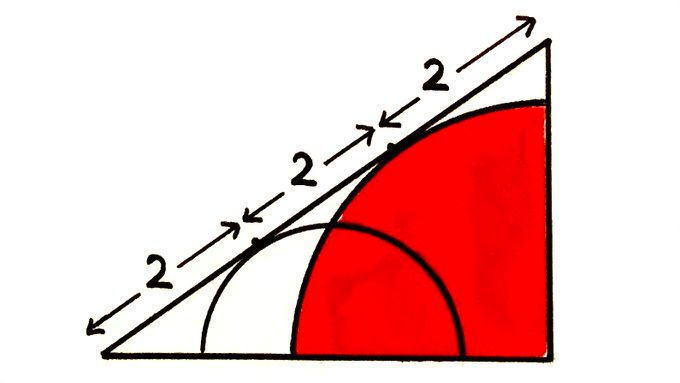
A right angled triangle with a filled red quarter circle with centre at the right angle and which is tangential to the hypotenuse. The hypotenuse is divided into three equal parts, each labelled "2". The point of tangency of the quarter circle is at a division point, with one part above and two parts below. Also in the diagram is a semi-circle which has centre on one of the non-hypotenuse sides and which meets tangentially the hypotenuse at the other division point.

I have a query about one of @catrionaagg.bsky.social 's puzzles. The goal is the area of the red quarter circle.

I have a solution that *doesn't* use the semi-circle. Am I missing something, or is that semi-circle irrelevant?

#geometrypuzzles

notes.mathforge.org/notes/publis...

TL;DR - too long, didn't read
BP;CR - behind paywall, couldn't read
AI;WR - AI generated slop, won't waste my time reading

For some reason, linking directly to an image doesn't fetch a preview of that image. That's annoying. Anyway, here's the image for that puzzle.

#mathsky #geometrypuzzles

Clearly Reviewer 2 didn't get the memo and thought they were Reviewer 1 here.

The fun is in the trying ... but also in the joining in, so post your working!

Sometimes I struggle to name @catrionaagg.bsky.social 's puzzles.

Sometimes I don't.

notes.mathforge.org/notes/publis...

#mathsky #geometrypuzzles

H/T @atulrana.bsky.social

And an ongoing h/t to @jemmaths.bsky.social - here's another in my search for category theory in school maths.

If the storm - or the cricket - is keeping you indoors and you just feel the need to read something about addition to take your mind off things ... I may have just what you're looking for.

loopspace.mathforge.org/CountingOnMy...

#mathsky #UKMathsChat #ITeachMaths

Oooh ... @tmip.bsky.social next animation prompt is "Hilbert Curves". Might have a go at that ...

But, does it have to be *Hilbert* - can I go for a different space-filling curve?

#mathsky

screenshot of resourceaholic.com

New post!

As promised, I've made a new resource library for GCSE Statistics: www.resourceaholic.com/2025/08/gcse...

#ukmathschat #gcsestatistics #mathstoday

4. Park in public spaces for free (up to a generous time limit). Removed a huge worry about getting a ticket at school pick-up!
5. Free charging *everywhere*. Supermarkets, swimming pools, museums. "Get a dozen eggs, and while you're there - charge the car!"
6. Clean energy.

1. No sales tax. This was *huge*; car sales tax in Norway can be more than 100%. So half of the cost-to-purchaser was tax. To put it another way, by buying electric you *double* your purchasing power.
2. No road tax.
3. Drive in bus lanes. The commute to school was *so* much easier!

Having been resident in Norway at the start of the modern electric car age, this doesn't surprise me. Nor does it happen by accident. Here are some of the incentives that the Norwegian government put in place for electric cars (some may no longer be in place):

Happy Birthday!

(My theory - as a parent - is that birthday's should be measured on a logarithmic scale. We celebrate the first day, first week, first month ... then by the time we get to my age it's "does it have a 0 in it?")

Okay, *now* I believe you're there!

AI at IMO 2025: a round-up Setting the scene The 2025 International Mathematics Olympiad has come and gone. Reminder: this is an exam for high-school kids across the world (each country typically sends six kids), comprising …

Thoughts on AI and the IMO.

xenaproject.wordpress.com/2025/08/03/a...

Ha! Was just going to say exactly this!

To adapt a common saying: "I Bergen, regner det kun to gang i uka - en gang i tre dager og en gang i fire."

(Apologies for the rusty Norwegian - it's been a while)

"I hold your hand in mine, dear"

Yesterday I spent a fascinating morning talking maths with a group of GPs. All professions require some level of numeracy, but doctors face particular challenges when communicating mathematical ideas.
I've written up a short blog: robeastaway.com/blog/gp-maths

The striking anomaly of repeating 3 questions in Papers 1 and 2 and the consequent omission of multiple core topics that were tested in all previous years makes the Pearson Maths A Level distinctly different and therefore "not comparable" to previous years.

#MathsToday #AlevelMaths #UKMathsChat

Only one of these is actually part of the circle ...

+1 for a teacher version

#mathsky #ITeachMaths

At least you get free wifi so that you can send them emails asking if breakfast is included!

Today I learned that Oxford has a (replica of Cambridge's) Mathematical bridge!

To go with its knock-off Bridge of Sighs, no doubt.

They'll be telling me next that the Rainbow Bridge is actually copied from some old viking myth.

#mathsky #UKMathsChat

Today I learned that Oxford has a (replica of Cambridge's) Mathematical bridge!

To go with its knock-off Bridge of Sighs, no doubt.

They'll be telling me next that the Rainbow Bridge is actually copied from some old viking myth.

#mathsky #UKMathsChat