joshmaxsilverman.bsky.social

Can you meet me at the mall? What is the greatest number of friends you're likely to meet if everyone fails to coordinate?

for more details, and my calculation of the setup questions, see joshmaxsilverman.github.io/2025-07-22-f... @xaqwg.bsky.social

the two approximations i make point in opposing directions, so it makes sense that they somewhat cancel, but the result seems too good for coincidence. i suspect it is a glimpse of a deeper calculation that takes into account the time correlation of the excitations.

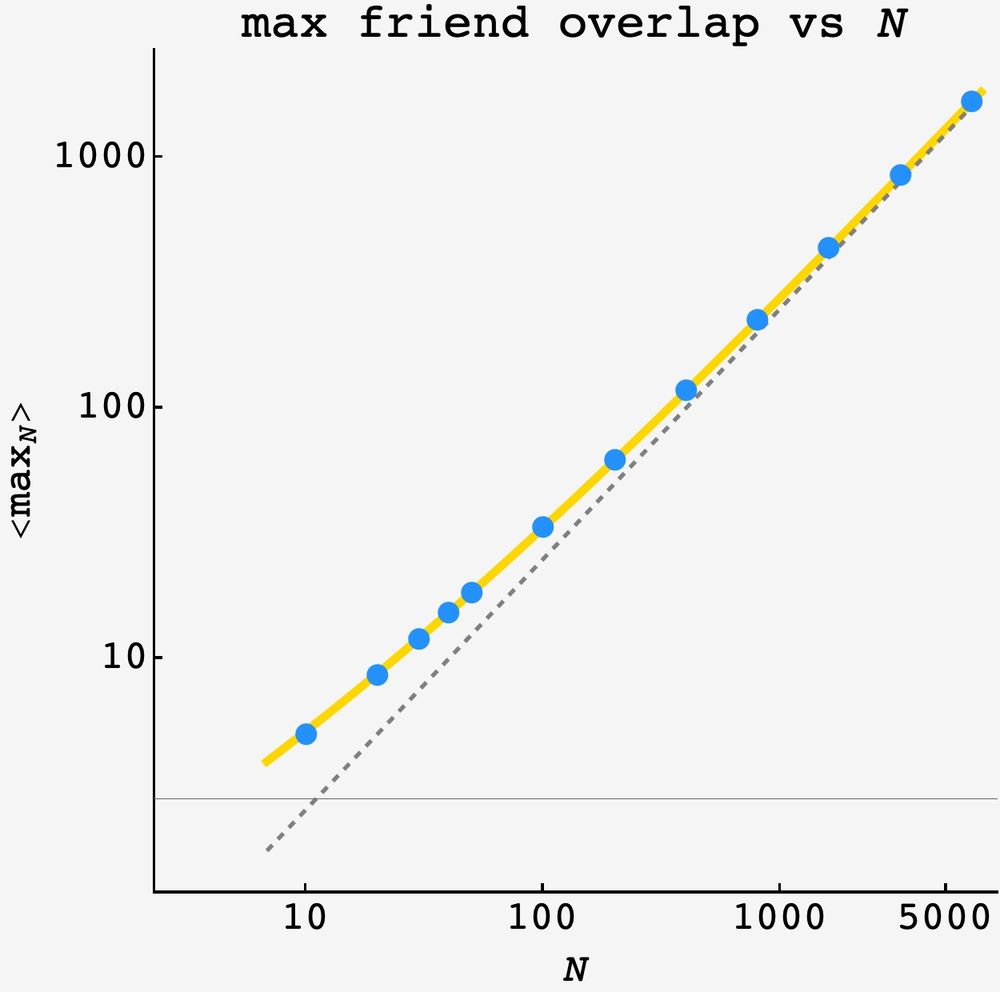
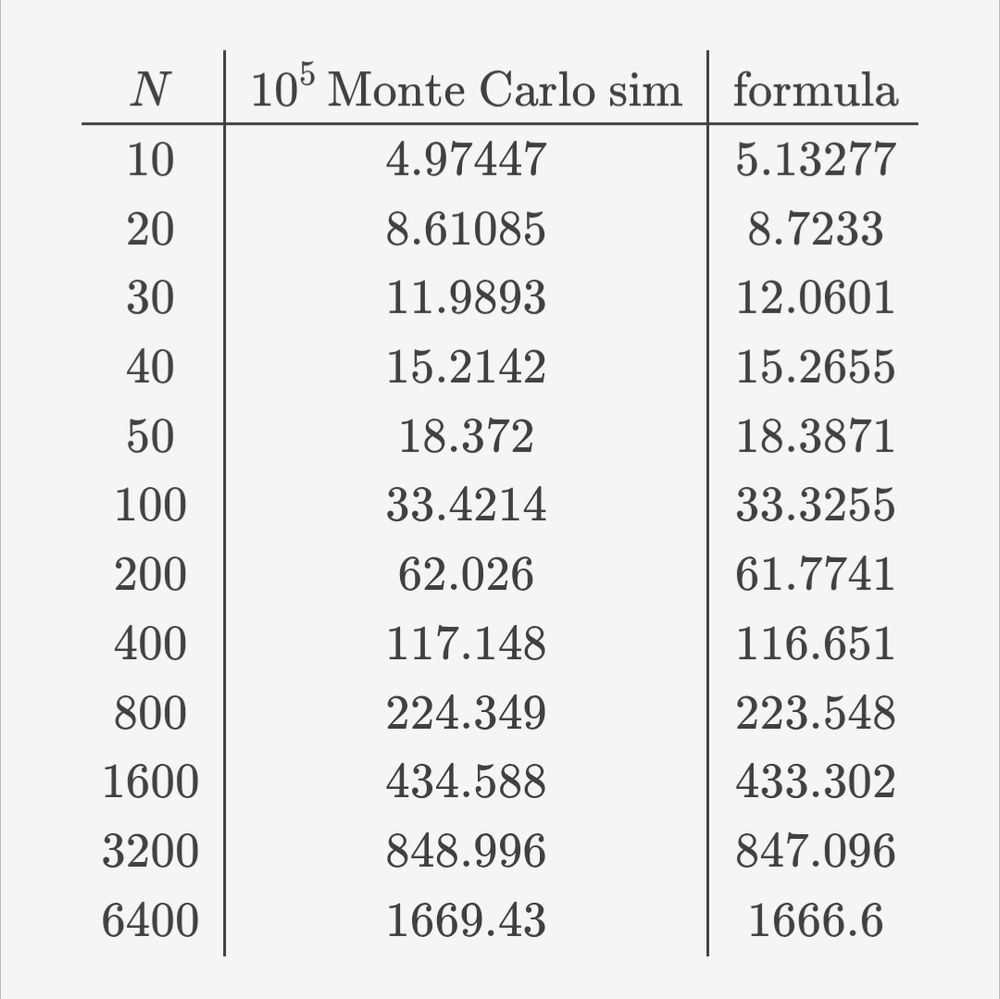
this captures the behavior closely, starting at about 10 friends.

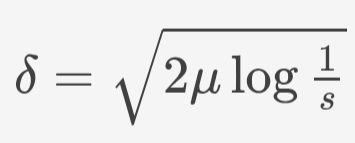
i then asked, at what k would we expect such an excitation to spawn once in an hour. this led to a remarkable formula for the excitation δ = (k-μ)

on average we'd expect N/4 friends in any 15 min interval. to probe the extremes, I made the approximation that each interval is an independent poisson process. I calculated the probability that such a window would have an excitation to k friends, and found the expected lifetime of such an interval.

in #thisweeksfiddler we are asked to find the expected maximum number of friends who are at the mall at the same time, given that they all go at a random 15 min window over an hour. i wondered about the large N behavior.

glad to pay you back for your non-vector solution to the tilted plot problem.

see https://joshmaxsilverman.github.io/2025-05-23-fiddler-river-fiddlish/ for more details @xaqwg.bsky.social

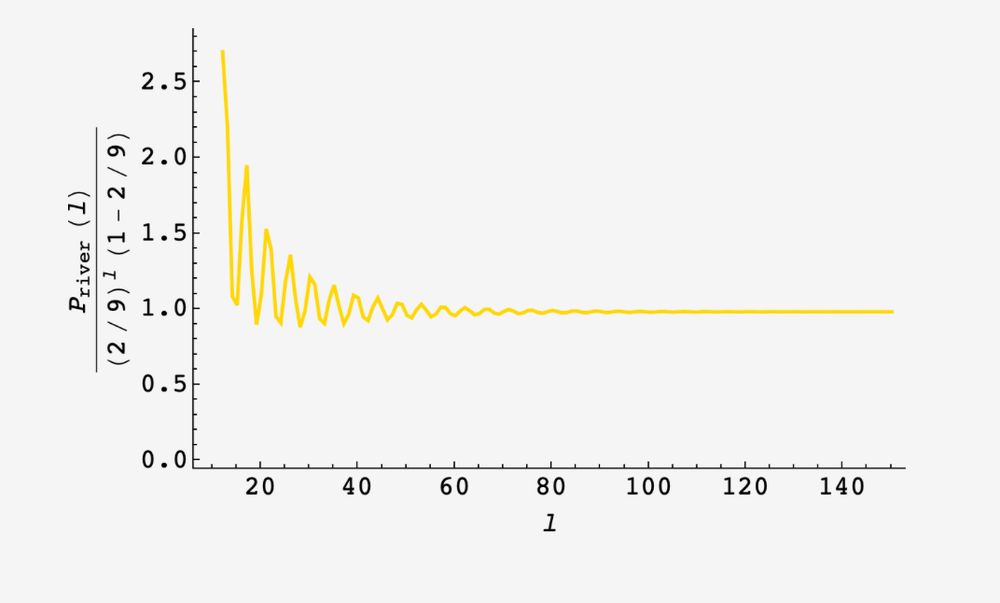
interestingly, the probability of a river of length ℓ is well approximated by the naive approximation times an extra factor of 2/9

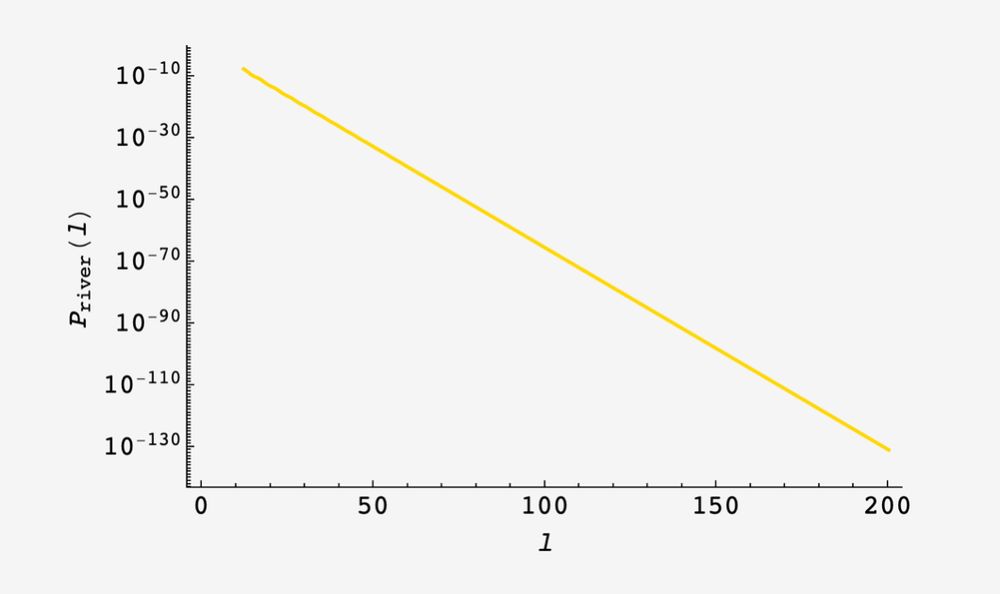
with this in hand, we can calculate the probability that the river has length ℓ

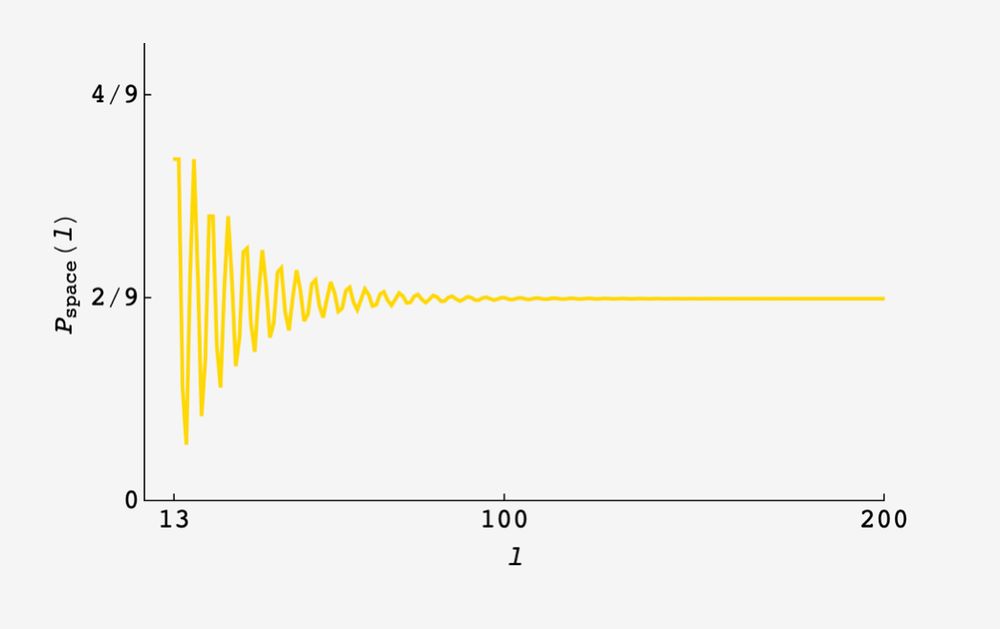
this oscillates around the long-distance value 2/9 before settling down

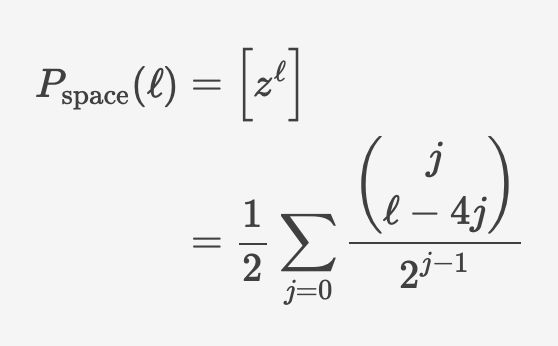
using generating functions, we can find an exact expression for the chance position ℓ is a space

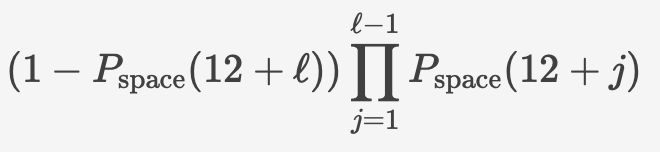
with this in hand, we can calculate the chance of a length ℓ river like

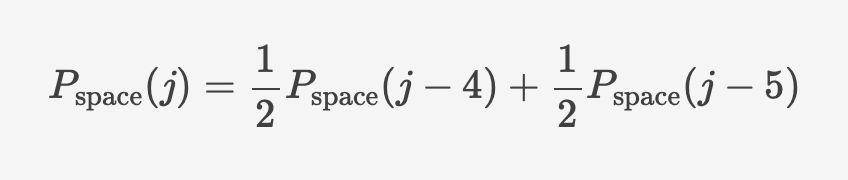
the chance position ℓ has a space is the chance position (ℓ-4) was a space times the chance a 3-letter word was used plus the chance position (ℓ-5) was a space times the chance a 4-letter word was used.

each line is very long, so we can just find the probability the a given line has a space at position ℓ.

in #thisweeksfiddler, we ask how long, on average, are coincidental diagonals of contiguous spaces in books written using 50% 3-letter, 50% 4-letter words with monospaced font.

for more details: https://joshmaxsilverman.github.io/2025-05-18-fiddler-counting-bipyramid/
@xaqwg.bsky.social

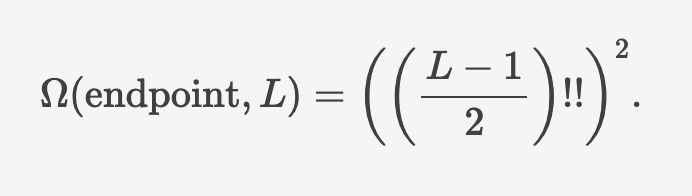
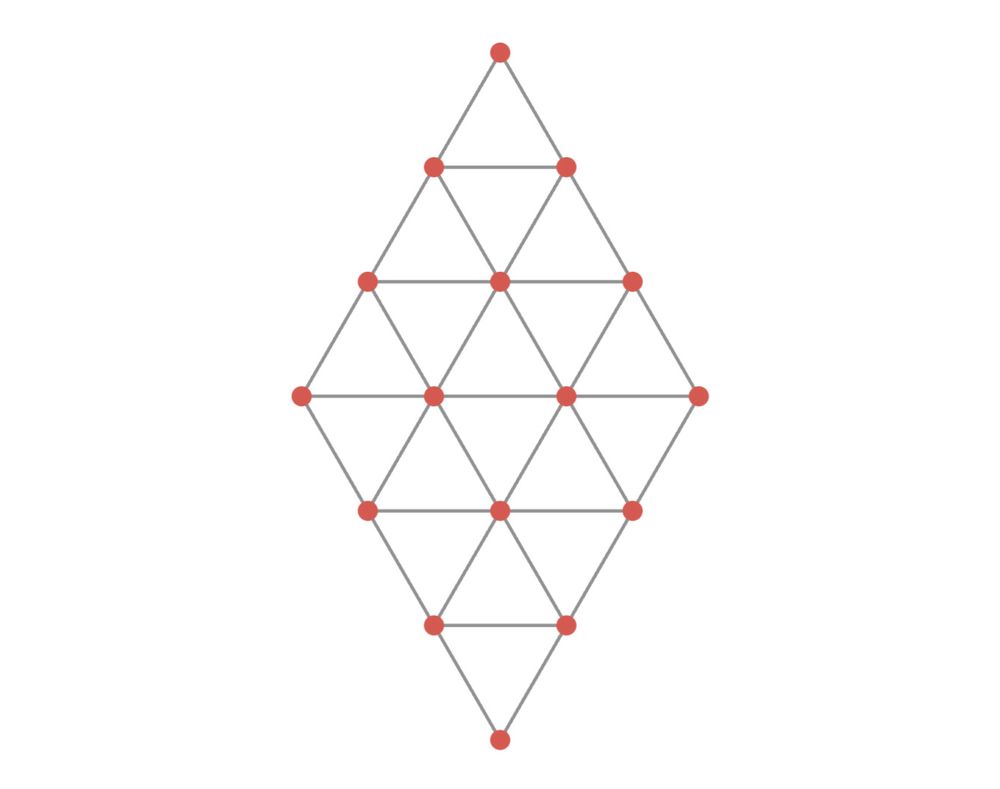
for the puzzle depicted, this is just 2*2*4*4*6*^ = 2,304 and in general, for an L-layer puzzle it is

paths from one node to another in a flat layer are unique, so sidestepping doesn't change the multiplicity. a path can enter/exit a layer at any node. since two edges emerge from any given node, the number of paths is just the product of the number of edges emerging at each layer.

we are also given a 2D version of the problem, which can be done with the same computational approach but can also be done analytically.

putting it all together, we can run Ω(bottom point) which gives 1,093,007,025 for the 7-layer bipyramid.

within a layer, pick a corner and call it row = 0, index = 0. all nodes can therefore be labelled by their row, index, and layer. in this scheme, vertical neighbors of node (r,i,l) in the upper half are ((r,i,l-1), (r-1,i,l-1), (r-1,i-1,l-1)) with the row/index shifts reversed in the lower half.

finally we can find T(i<-j, l) by searching within the layer. this leaves determining the vertical neighbors for any given node which can be seen by overlaying one layer of the pyramid on the one below.

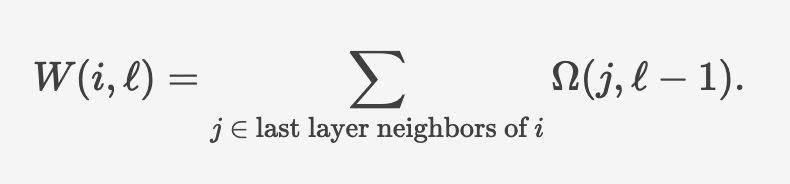
we can find the number of ways to enter a layer at node i as the sum of ways to exit the last layer from one of its neighbors

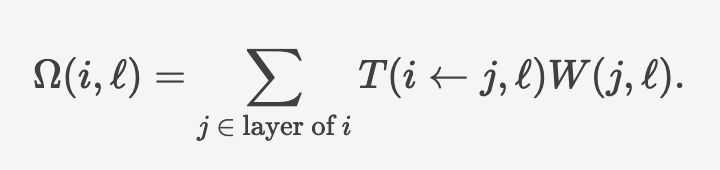
at each layer, a path enters at a node, and moves to exit from any other node. therefore, the number of ways Ω(i) to exit a layer from node i is the number of ways W(j) to enter the layer at node j times the number of ways to move from j to i within their layer, without repeating an edge T(i <- j)

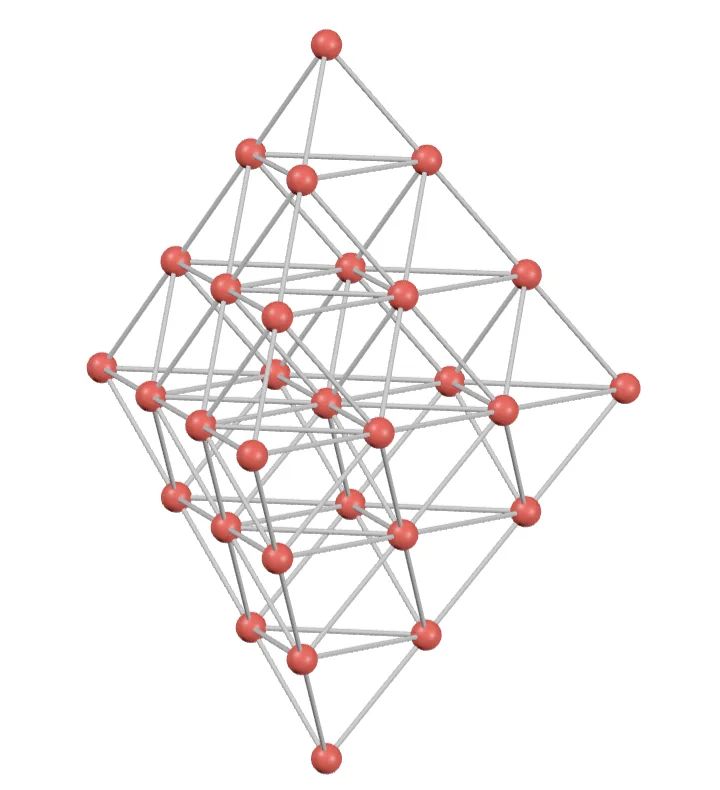
In #thisweeksfiddler we're asked to count the paths down a bipyramid, starting at the top and exiting the bottom, without taking any edge twice.

the standard credit simplifies to a similar expression, 7/6 + H_N

the standard credit is actually a bit more complicated, and is treated in the post.

joshmaxsilverman.github.io/2025-05-04-f...

@xaqwg.bsky.social

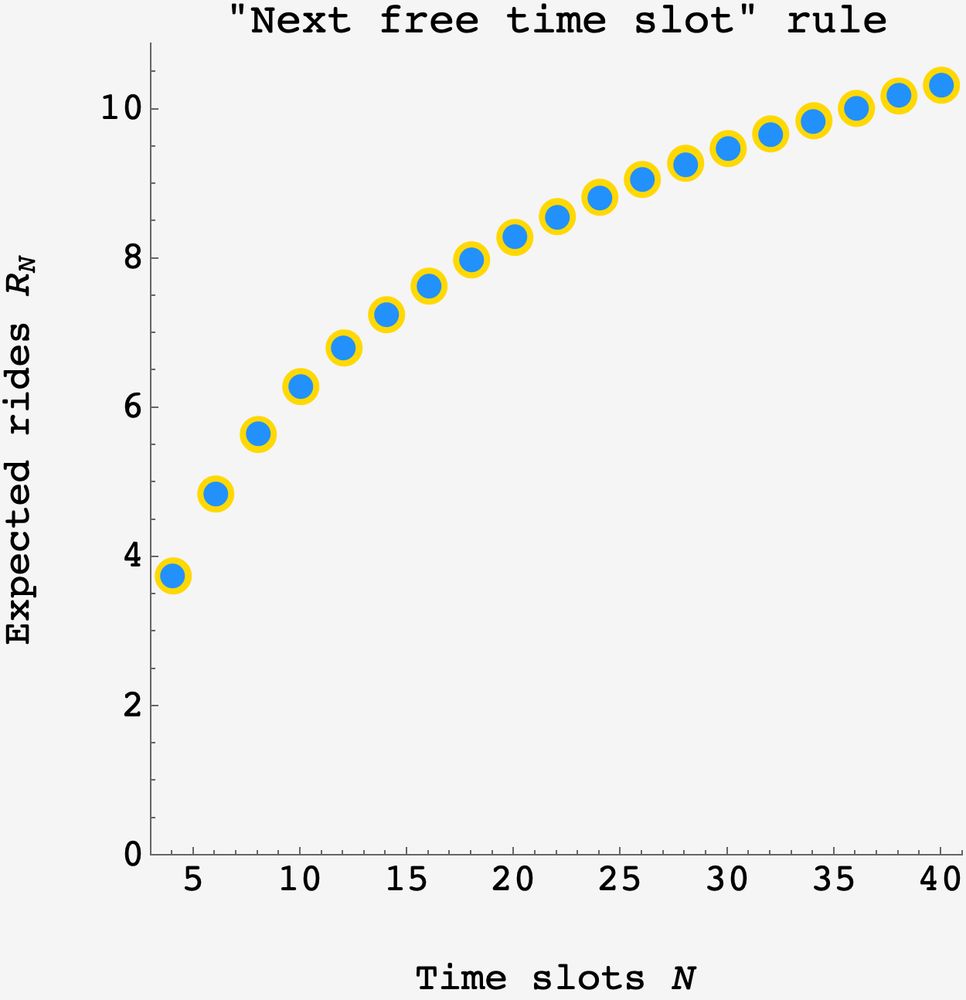
recursing down to the the case of 3 time slots, which gives 3 rides by definition, this shows the expected number of rides is (3H_N - 5/2) where H_N is the Nth harmonic number (1 + 1/2 + ... + 1/N).

the blue points are the result of a 1E6 round simulation and the gold point are the formula above.

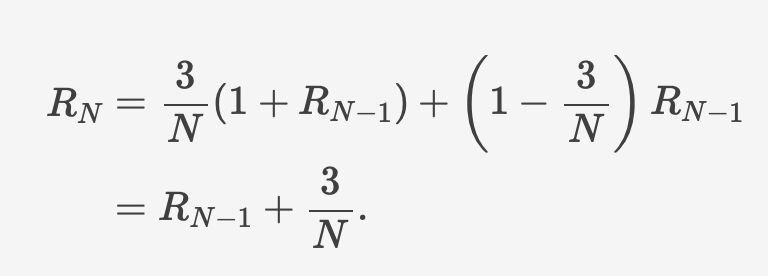
this means that the expected number of rides with N time slots is the expected number of rides with (N-1) time slots plus the expected number of times the first time slot is occupied.