Tycho van der Ouderaa

Today at NeurIPS, we’ll be presenting our Noether's Razor paper! 📜✨
📅 Today Fri, Dec 13
⏰ 11 a.m. – 2 p.m. PST
📍 East Exhibit Hall A-C, #4710 (ALL the way in the back I believe!)
w/ @mvdw.bsky.social @pimdh.bsky.social
Come say hi! 👋

For those interested, I will be giving a short talk today about our recent work “Pyramid Vector Quantization for LLMs” at the Microsoft booth at NeurIPS, starting at 10:30.

Sure!

Noether's razor: Learning Conserved Quantities Symmetries have proven useful in machine learning models, improving generalisation and overall performance. At the same time, recent advancements in learning dynamical systems rely on modelling the un...

Interested?

Come check out our poster at NeurIPS 2024 in Vancouver.
East Exhibit Hall A-C #4710, Fri 13 Dec 1-4 pm CST
Link: neurips.cc/virtual/2024...

Paper/code: arxiv.org/abs/2410.08087

Thankful to co-authors @mvdw.bsky.social and @pimdehaan for their joint supervision of this project

🧵16/16

Noether's razor allows symmetries to be parameterised in terms of conserved quantities and enables automatic symmetry at train time. This results in more accurate Hamiltonians that obey symmetry and trajectory predictions that remain more accurate over longer time spans.🧵15/16

Our work demonstrates that approximate Bayesian model selection can be useful in neural nets, even in sophisticated use cases. We aim to further improve the efficiency and usability of neural model selection, making it a more integral part of training deep neural nets. 🧵14/16

If one wishes, we could extend to non-quadratic conserved quantities to model non-affine actions. More free-form conserved quantities would require ODE-solving instead of the matrix exponential and have more parameters, which could complicate the Bayesian model selection.🧵13/16

Further, this does not limit the shapes of symmetry groups we can learn. For instance, we find the Euclidean group, which is itself a curved manifold with non-trivial topology.🧵12/16

We use quadratic conserved quantities, which can represent any symmetry with an affine (linear + translation) action on the state space. This encompasses nearly all cases studied in geometric DL. 🧵12/16

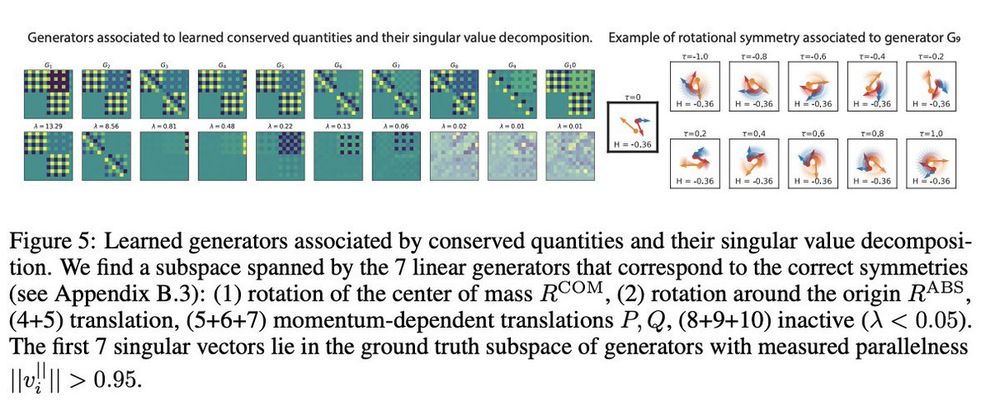
On more complex N-body problems, our method correctly discovers the correct 7 linear generators which correspond to the correct linear symmetries of rotation around center of mass, rotation around the origin, translations, and momentum-dependent translations. 🧵11/16

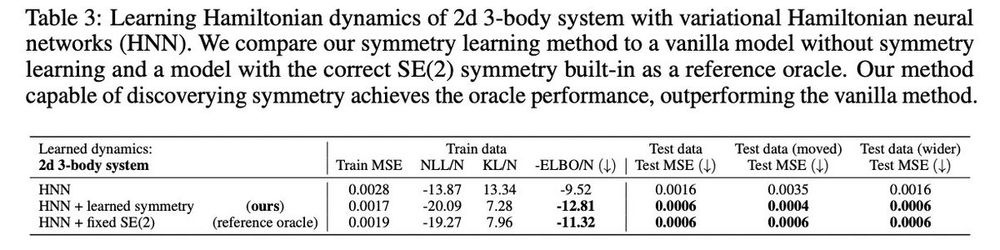
By learning the correct symmetries, the jointly learned Hamiltonians are more accurate, directly improving trajectory predictions at test time. We show this for n-harmonic oscillators, but also more complex N-body problems (see table below). 🧵10/16

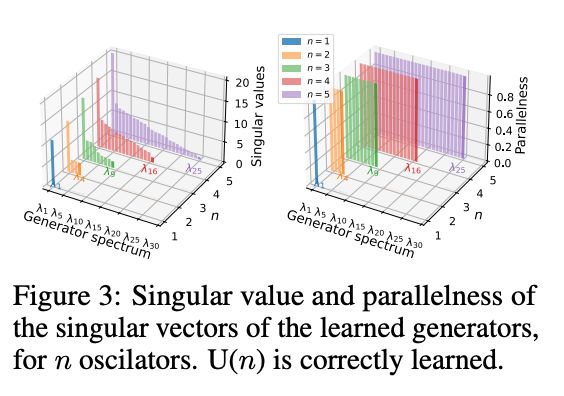
We verify the correct symmetries and group dimensionality are learned by inspecting parallelism, singular vectors, and transformations associated with learned generators. For instance, we correctly learn the n² dimensional unitary Lie group U(n) on N-harmonic oscillators.🧵9/16

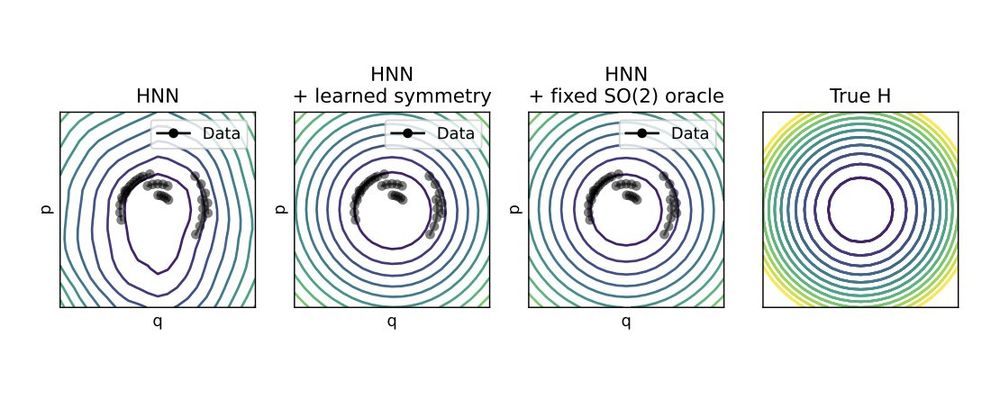
Our method discovers the correct symmetries from data. Learned Hamiltonians that obey the right symmetry generalise better as they remain more accurate in larger areas of the phase space, depicted here for a correctly learned SO(2) on a simple harmonic oscillator. 🧵8/16

Noether's razor jointly learns conservation laws and the symmetrised Hamiltonian on train data, without requiring validation data. By relying on differentiable model selection, we do not introduce additional regularizers that require tuning.🧵7/16

As far as we know, this is the first case in which Bayesian model selection with VI is successfully scaled to deep neural networks, an achievement in its own right, whereas most works so far have relied on Laplace approximations. 🧵6/16

We scale to deep neural networks using Variational Inference (VI). To obtain a sufficiently tight bound for model selection, we avoid mean-field and instead use efficient matrix normal posteriors and closed-form updates of prior and output variance (see tricks in App. D). 🧵5/16

We jointly learn the Hamiltonian and conserved quantities with Bayesian model selection by optimising marginal likelihood estimates. This yields a Noether's Razor effect favouring simpler symmetric solutions if this describe data well, avoiding collapse into no symmetry. 🧵4/16

We let our Hamiltonian neural network be a flexible deep neural network that is symmetrized by integrating it over the flow induced by a set of learnable conserved quantities. This construction allows us to define a flexible function with learnable symmetry. 🧵3/16

Noether's theorem states that symmetries in a dynamical system have an associated conserved quantity, i.e. an observable that remains invariant over a trajectory. We use this result to parameterise symmetries in Hamiltonian neural networks in terms of conserved quantities. 🧵2/16

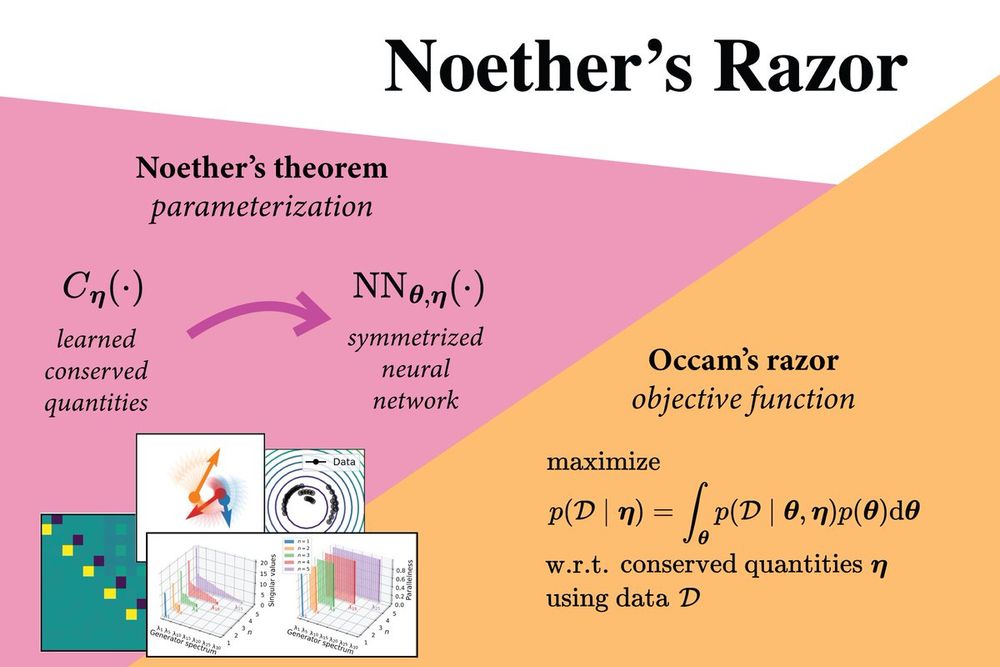
🌟Noether's razor⭐️ Our NeurIPS 2024 paper connects ML symmetries to conserved quantities through a seminal result in mathematical physics: Noether's theorem. We can learn neural network symmetries from data by learning associated conservation laws. Learn more👇. 1/16🧵

I made a starter pack for Bayesian ML and stats (mostly to see how this starter pack business works).

Let me know whom I missed!

go.bsky.app/2Bqtn6T

I made a starter pack for researchers in probabilistic machine learning.

DM/reply if you want to be added!

go.bsky.app/DuCtJqC