Felix Koehler

APEBench: A Benchmark for Autoregressive Neural Emulators of PDEs We introduce the Autoregressive PDE Emulator Benchmark (APEBench), a comprehensive benchmark suite to evaluate autoregressive neural emulators for solving partial differential equations. APEBench is b...

We will use APEBench to train, test and benchmark it in an advection scenario against a feedforward ConvNet.

arxiv.org/abs/2411.00180

YouTube video by Machine Learning & Simulation Transformer Neural Operator in JAX

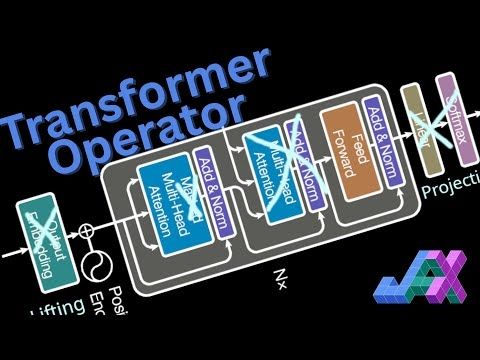
Check Out my latest video on implementing an attention-based neural operator/emulator (i.e. a Transformer) in JAX:
youtu.be/GVVWpyvXq_s

PRDP: Progressively Refined Differentiable Physics The physics solvers employed for neural network training are primarily iterative, and hence, differentiating through them introduces a severe computational burden as iterations grow large. Inspired by...

Travelling to Singapore next week for #ICLR2025 presenting this paper (Sat 3 pm nr. 538): arxiv.org/abs/2502.19611

DM me (Whova, Email or bsky) if you want to chat about (autoregressive) neural emulators/operators for PDE, autodiff, differentiable physics, numerical solvers etc. 😊

machine-learning-and-simulation/english/simulation_scripts/lorenz_lyapunov_spectrum_jax.ipynb at main · Ceyron/machine-learning-and-simulation All the handwritten notes 📝 and source code files 🖥️ used in my YouTube Videos on Machine Learning & Simulation (https://www.youtube.com/channel/UCh0P7KwJhuQ4vrzc3IRuw4Q) - Ceyron/machine-learn...

Notebook: github.com/Ceyron/machi...

YouTube video by Machine Learning & Simulation Full Lyapunov Spectrum of Chaotic Lorenz System using JAX

Check out my latest video on approximating the full Lyapunov spectrum for the Lorenz system: youtu.be/Enves8MDwms

Nice showcase of #JAX's features:
- `jax.lax.scan` for autoregressive rollout
- `jax.linearize` repeated jvp
- `jax.vmap`: automatic vectorization

Art.

YouTube video by Machine Learning & Simulation APEBench Talk @ Pasteur Labs Journal Club

Today, I had the chance to present my #NeurIPS paper "APEBench" @SimAI4Science . You can find the recording on YouTube: youtu.be/wie-SzD6AJE

To get started with APEBench install it via `pip install apebench` and check out the public documentation: tum-pbs.github.io/apebench/

Finally, there are so many cool experiments we did to find insights in neural emulators, to highlight limitations they inherit from the numerical simulator counterparts, etc. You find all the details in the paper: arxiv.org/pdf/2411.00180

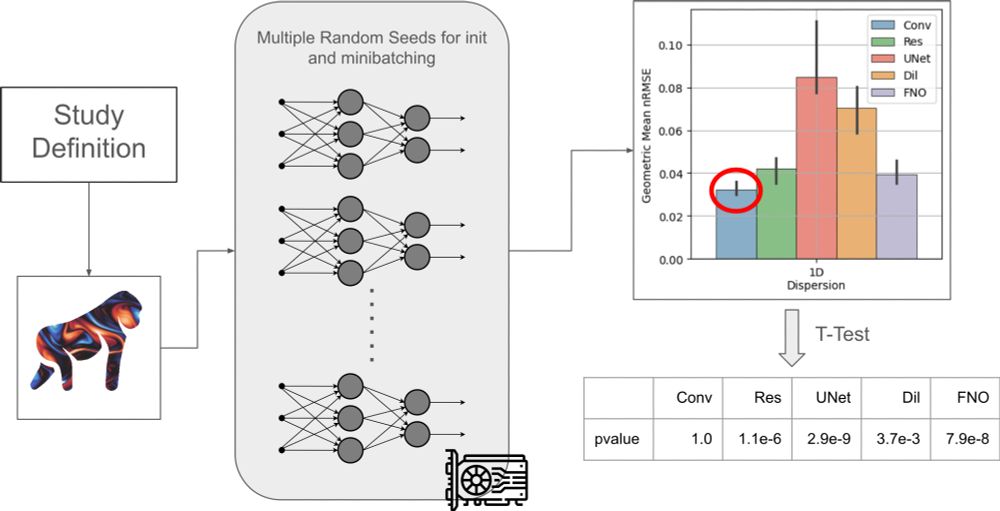
And to enforce good practices APEBench is designed around controllable deterministic pseudo-randomness that allows for straightforward run of seed statistics that can be used to perform hypothesis tests.

Another important contribution is that APEBench defines most of its PDEs via a new parameterization that we call "difficulties". Those allow for expressing a wide range of different dynamics with a reduced and interpretable set of numbers.

This allows for investigating how unrolled training helps with long-term accuracy.

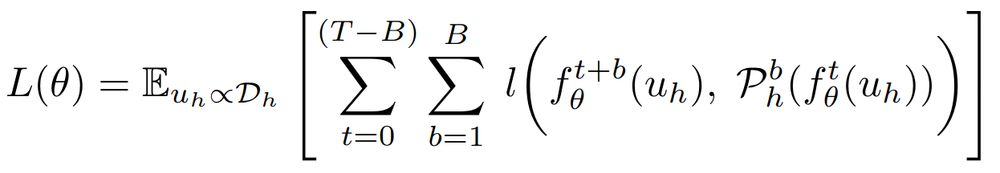
Temporal Axis also means various configurations of how emulator and simulator interact during training, for example, in terms of supervised unrolled training. We generalize many approaches seen in the literature in terms of unrolled steps T and branch steps B.

One core motivation for APEBench was the temporal axis in emulator learning (hence the "autoregressive" in APE). We focus on rollout metrics and sample rollouts to truly understand temporal generalization via long-term stability and accuracy in more than 20 metrics.

We, of course, also ship a wide range of popular emulator architectures, all of them implemented in JAX and designed agnostic to spatial dimension and boundary conditions. If you don't like APEBench (which I cannot imagine 😉), they are also available individually: github.com/Ceyron/pdequ...

GitHub - Ceyron/exponax: Efficient Differentiable n-d PDE solvers in JAX. Efficient Differentiable n-d PDE solvers in JAX. Contribute to Ceyron/exponax development by creating an account on GitHub.

The solver is also available as an individual package: Exponax: github.com/Ceyron/exponax

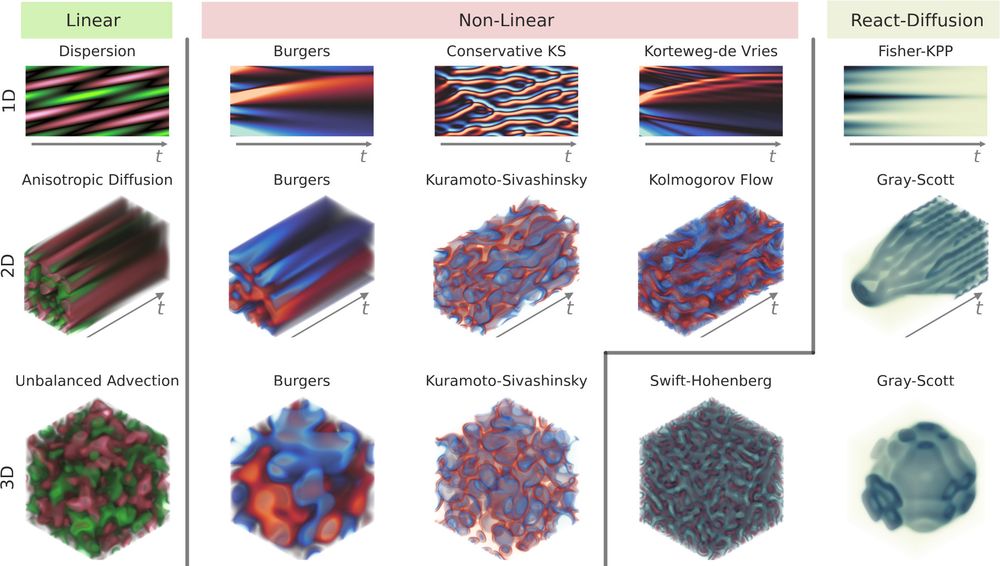
This numerical solver is based on Fourier-pseudo spectral ETDRK methods, one of the most efficient numerical techniques to solve semi-linear PDEs on periodic boundaries for which we provide a wide range of pre-defined configurations (46 as of the initial release).

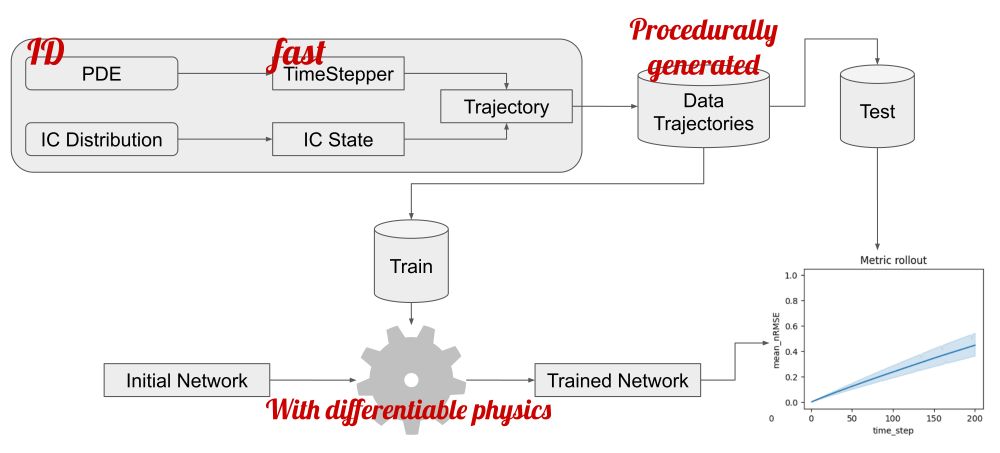
With it, we can _procedurally_ generate all data ever needed in seconds on a modern GPU --- yes, this means you do not have to download hundreds of GBs of data. Installing the APEBench Python package (<1MB) is sufficient. 😎

The key innovation is to tightly integrate a classical numerical solver that produces all the synthetic training data with incredible efficiency and allows for easy scenario customization.

Thanks @munichcenterml.bsky.social for highlighting my recent #NeurIPS paper: APEBench,
a new benchmark suite for autoregressive emulators of PDEs to understand how we might solve the models of nature more efficiently. More details 🧵

Visual summary on project page: tum-pbs.github.io/apebench-pap...

Our online book on systems principles of LLM scaling is live at jax-ml.github.io/scaling-book/

We hope that it helps you make the most of your computing resources. Enjoy!

I’d like to thank everyone contributing to our five accepted ICLR papers for the hard work! Great job everyone 👍 Here’s a quick list, stay tuned for details & code in the upcoming weeks…

Scholar Inbox is amazing. Thanks for the great tool 👍

Amazing ❤️
Thanks for sharing and the kind words.

YouTube video by Machine Learning & Simulation APEBench Quickstart

I created a video to help you get started using the APEBench suite (my recent #neurips paper) to benchmark autoregressive neural emulators for PDEs with a simple ConvNet emulation of 1D advection: youtu.be/q8fjQ4ZFynw

A screenshot of the YouTube channel homepage with "25K subscribers" highlighted in a red hand-drawn circle.

Happy new year! 🎉 Two days ago we entered 2025 and just in time the channel surpassed 25k subscribers. Wow! Thanks to everyone for their kind words and support along the way: www.youtube.com/channel/UCh0...

YouTube video by Machine Learning & Simulation Largest Lyapunov Exponent using Autodiff in JAX/Python

Check out my latest video on approximating the largest Lyapunov exponent of a dynamical system by integrating a tangent linear perturbation dynamic via autodiff in JAX: youtu.be/zRMBIkpcuu0

Very neat use-case of forward-mode AD for efficient Lyap approximation.

Really enjoyed our closing hockey game 😊

Automatic differentiation in forward mode computes derivatives by breaking down functions into elem operations and propagating derivatives alongside values. It’s efficient for functions with fewer inputs than outputs and for Jacobian-vect prod, using for instance dual numbers.

Now presenting APEBench at #NeurIPS in West #5407.