Justin Lanier

Both give the rating 0/0.

Similarly, Pennsylvania's top portion and its exclusive definition. I genuinely thought that was the point of those shapes before I recognized the shapes as state outlines. 😂

Funnily enough, the top portion of Ohio might well qualify as a trapezoid by its own inclusive definition! 😄

How come?

Every bubble is popped on one side of it and raised on the other side. 😜

vghay also pkease

Sum Fun

Lovely!

Or—and hear me out here—give those assignments, if you think they are worth students doing, and make them a completion grade. (Or even, at times, for no grade at all.)

😄

*our

I presented on this problem today!

You can find the slides here:
docs.google.com/presentation...

I don't use speaker notes (just vibes) but I think a recorded version exists and I'll try to link to it if/when I can.

cc #iTeachMath ♾️ bcc #MathSky 🧮

There should also be a new defensive position to prevent baserunners from using this shortcut. A "shortcutstopper" or something.

Yesterday I spent a fascinating morning talking maths with a group of GPs. All professions require some level of numeracy, but doctors face particular challenges when communicating mathematical ideas.
I've written up a short blog: robeastaway.com/blog/gp-maths

....and nickel...

You are almost—but not quite—off the grid. 😄 Hope you are having a nice getaway!

aluminum

Make more yourself at this link: demonstrations.wolfram.com/TilingTheHyp...

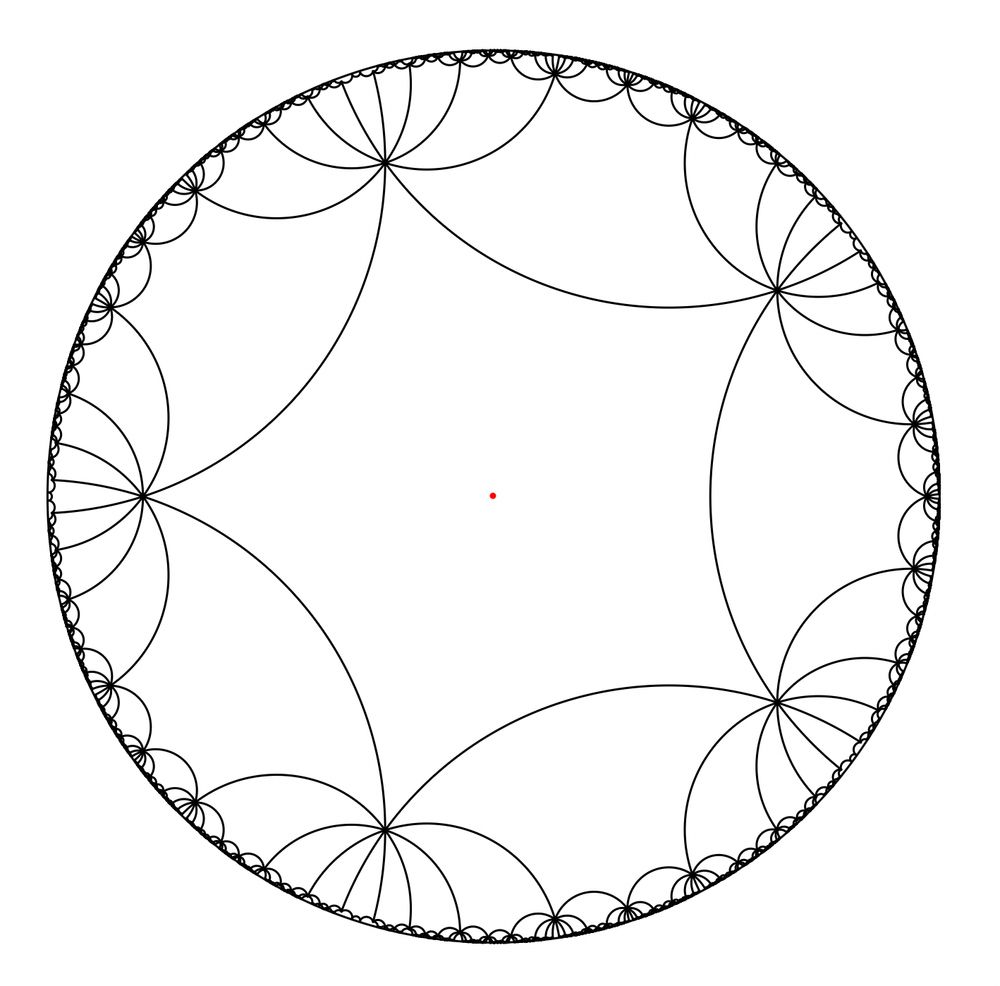
A tiling of the hyperbolic plane in the disk model with 10 regular pentagons at every vertex; this time the image is centered on one of the pentagons.

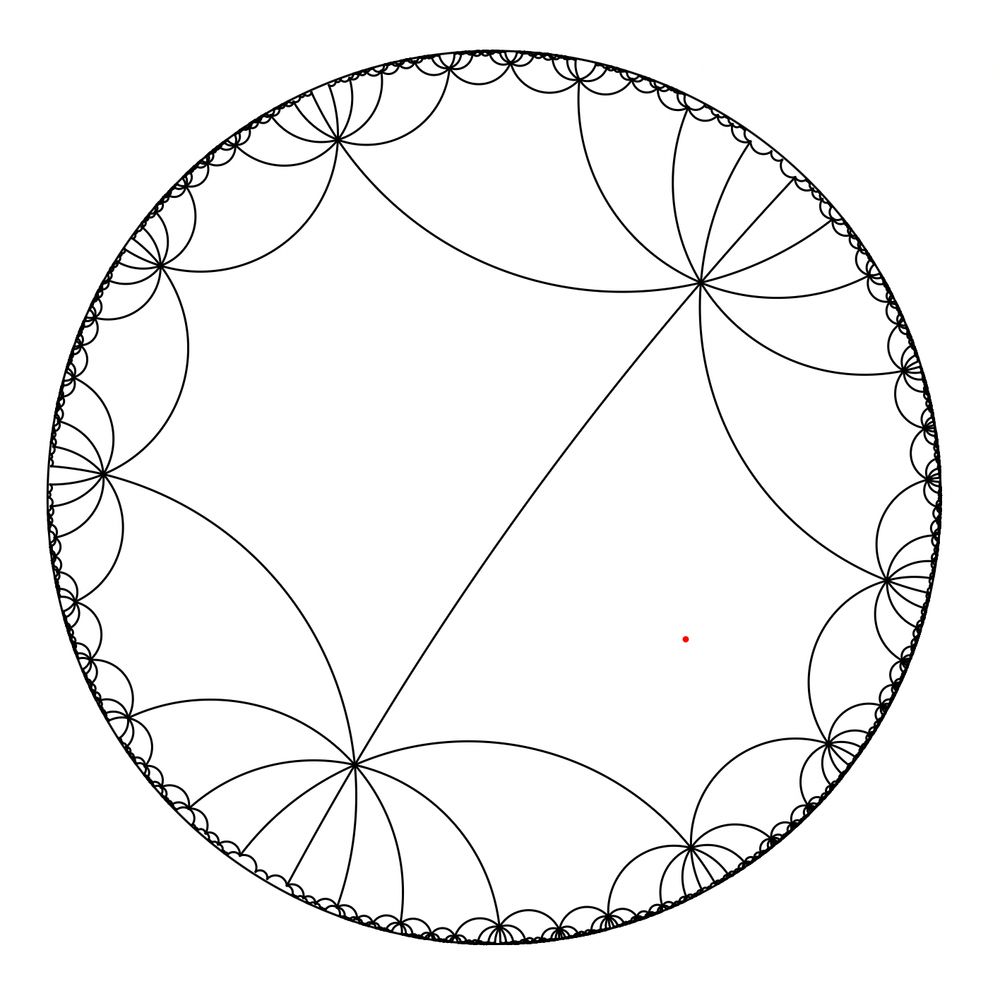
A tiling of the hyperbolic plane in the disk model with 10 regular pentagons at every vertex.

from “Does one have to be a genius to do maths?” by Terry Tao: "The answer is an emphatic NO. In order to make good and useful contributions to mathematics, one does need to work hard, learn one’s field well, learn other fields and tools, ask questions, talk to other mathematicians, and think about the “big picture”. ... The number of interesting mathematical research areas and problems to work on is vast – far more than can be covered in detail just by the “best” mathematicians, and sometimes the set of tools or ideas that you have will find something that other good mathematicians have overlooked, especially given that even the greatest mathematicians still have weaknesses in some aspects of mathematical research."

Independent of thinking about AI, Terry Tao himself has an interesting and encouraging perspective regarding that first question:

Excited to say, "looking forward to it!" 🙌

Misread that as "origami".

It's okay, you can rate my response a 0%. 😆 Thanks for putting up with it.

Kind of joking, but just using a discrete metric: how far is this rectangle from being a square? Well, if it's not a square, it is 100% far from being a square; and if it *is* a square, then it is 0% far from being a square. It's like a graph theory metric: you are either at the spot, or not.

Probably 100% most of the time, but every once in a while 0%.

😅 Welcome! At least the weather ought to be relatively nice during your visit. Looking forward to your Sydney Ideas event on Thursday!

International Visitor Program - Sydney Mathematical Research Institute IVP August 2023 applications are due 8 August 2023, for July 2024–June 2025 visits (general applicants) & March 2024–June 2025 for Australian citizens/PR & NZ citizens.

Applications are now open for our International Visitor Program, open to #mathematicians to visit Aus 🐨 between July '26-'June 27, or March '26-June -27 (Aus/NZ citizens)
📅 Apply by Aug 1, info:
mathematical-research-institute.sydney.edu.au/internationa...
Please share with your networks 🔁 #MathSky

Please mail me my earned Certificate 0 with Honors at your earliest convenience. 👨‍🎓

“21st century mathematics”: a free month-long online enrichment program for math teachers.

Info + register: bit.ly/21math2025

Video part 1: